题目内容
【题目】如图所示,在平面坐标系xOy的第一象限内有一半圆形区域,其半径为R,半圆的一条直径与x轴重合, O为该直径的一个端点。半圆内存在垂直纸面向里的匀强磁场,半圆外存在垂直纸面向外的匀强磁场,半圆内外磁场的磁感应强度大小都为B0,在坐标原点O处有一粒子源,沿x轴正方向不断发射出质量为m、带电荷量为+q的粒子,粒子的发射速度为大于零的任意值(不考虑相对论效应)。已知半圆形边界处存在特殊物质,当粒子由半圆内向半圆外运动时,粒子不受任何影响,但当粒子由半圆外向半圆内运动时,粒子就会被边界处的特殊物质吸收。不计粒子的重力和粒子间的相互作用力。

(1)求从O点发射的所有粒子中,不会从y轴正半轴射入第二象限的粒子的速度的取值范围; (已知:![]() )
)
(2)证明最终打在半圆形边界且被特殊物质吸收的粒子,在磁场中运动的总时间都相等,并且求出该时间;
(3)若第一象限内半圆形外区域的磁场存在一上边界y=a ,要想使所有粒子都不会从磁场上边界射出,则a至少为多大。
【答案】(1) ![]() (2)
(2) ![]() (3)2R
(3)2R
【解析】
(1)分析不进入第二象限的条件,然后根据几何关系及洛伦兹力作向心力来求解速度范围;
(2)画出打在半圆形边界的图,然后根据几何关系求得粒子运动的中心角,再根据粒子做圆周运动的周期求解时间;
(3)分析粒子运动轨迹,将粒子运动的最高点用半圆半径表示出来,即可求得a的最小值.
(1)如图甲所示;
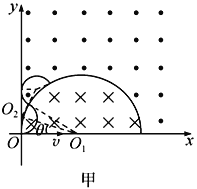
当粒子在半圆外做圆周运动恰好与y轴相切时,此时粒子的速度为最小值,设带电粒子在磁场内做匀速圆周 运动的轨道半径为r,轨迹圆心O2与半圆圆心O1连线与x轴之间的夹角为θ,由几何关系可知![]()
![]()
两式联立可得:θ=15°, r=Rtan15°
又![]()
得![]()
所以不会从y 轴正半轴射入第二象限的粒子的速度的取值范围为![]()
(2)如图乙所示做出某一速度粒子的轨迹,最终打在半圆边界,
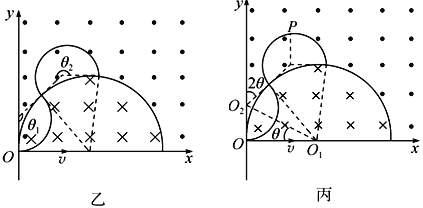
由几何关系可知: θ1+ θ2=360°
所以带电粒子在磁场中运动的总时间为![]()
(3)如图丙所示做出某一速度粒子的轨迹,设其最高点为P,轨迹圆心O2与半圆圆心O1连线与x轴之间的夹角为θ,由几何关系可得P距x轴的距离(也就是P点的纵坐标)为y![]()
又因为![]()
两式联立可得![]()
当θ=45°时,x取到最大值ymax=2R
所以想使所有粒子都不会从磁场上边界射出,a的最大值为amax=2R