题目内容
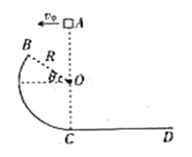
【题目】如图所示,固定在竖直面内的圆弧轨道![]() 与水平地面相切于
与水平地面相切于![]() 点,半径
点,半径![]() 与水平方向的夹角
与水平方向的夹角![]() 。一质量
。一质量![]() 的小物块(可视为质点)从
的小物块(可视为质点)从![]() 点正上方的
点正上方的![]() 点以大小
点以大小![]() 的速度水平向左抛出,恰好沿
的速度水平向左抛出,恰好沿![]() 点的切线方向进人并沿圆弧轨道运动,最终停在
点的切线方向进人并沿圆弧轨道运动,最终停在![]() 点。已知物块从
点。已知物块从![]() 点运动到
点运动到![]() 点历时t=1.2s,物块与地面间的动摩擦因数
点历时t=1.2s,物块与地面间的动摩擦因数![]() ,取
,取![]() ,
,![]() 。求:
。求:
(1)圆弧轨道的半径![]() ;
;
(2)物块到达![]() 点前瞬间的速度大小
点前瞬间的速度大小![]() 以及此时圆弧轨道对物块的支持力大小
以及此时圆弧轨道对物块的支持力大小![]() ;
;
(3)物块从![]() 点运动到
点运动到![]() 点的过程中,系统因摩擦产生的热量
点的过程中,系统因摩擦产生的热量![]() 。
。
【答案】(1)1.5m (2)6m/s;6.8N (3)3.7J
【解析】
(1)物块从A运动到B做平抛运动,根据平抛运动水平方向分速度不变,由B点速度的方向求出物块到达B点时的竖直分速度大小;根据水平方向的运动规律,求解圆弧轨道的半径R;(2)物块从C到D做匀减速运动,根据牛顿第二定律求得加速度,再由速度时间公式求物块到达C点前瞬间的速度大小![]() ,物体在C点时,由轨道的支持力和重力的合力提供向心力,由牛顿第二定律求得支持力。(3)由速度的分解法求得物块经过B点时的速度,再由能量守恒定律求系统因摩擦产生的热量Q。
,物体在C点时,由轨道的支持力和重力的合力提供向心力,由牛顿第二定律求得支持力。(3)由速度的分解法求得物块经过B点时的速度,再由能量守恒定律求系统因摩擦产生的热量Q。
(1)设物块抛出后在空中做平抛运动的时间为![]() ,作出此时的速度分析图如图所示:
,作出此时的速度分析图如图所示:
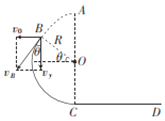
则物块到达B点时的竖直分速度大小为:![]()
由几何关系有:![]()
又水平方向有:![]()
解得:R=1.5m
(2)物块从C点运动到D点的过程中,根据牛顿第二定律有:![]()
由匀变速直线运动规律有:![]()
联立解得:![]()
物块刚到达C点时有:![]()
解得:N=6.8N。
(3)物块通过B点时的速度大小为:![]()
物块从B点到C点的过程中,根据能量守恒定律有:![]()
解得:Q=3.7J

练习册系列答案
相关题目