��Ŀ����
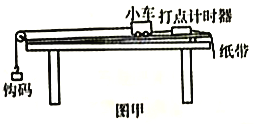
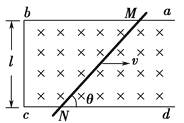
����Ŀ���㹻����ˮƽ���ʹ��Ҳ���һ���봫�ʹ��ϱ������е�![]() �⻬Բ�����������ΪM��2kg��Сľ�д���Բ����h=0.8m���ɾ�ֹ�ͷţ����ϴ��ʹ����������˶���1s��ǡ���봫�ʹ����ֹ��١����ʹ�ʼ�����ٶȴ�Сv��ʱ�����У�ľ���봫�ʹ�֮��Ķ�Ħ������Ϊ����0.2��ľ���봫�ʹ�������Ծ�ֹ���Ⱥ����T��5s����v0��10m/s���ٶ��ڴ��ʹ���������Ƴ�������ȫ��ͬ�Ĺ⻬С��С�������m��1kg����1������ľ��������������������в���б�����Ծ�ֹ����2�����������ʱ��t��0.5s��ľ��������ȡg��10m/s2����
�⻬Բ�����������ΪM��2kg��Сľ�д���Բ����h=0.8m���ɾ�ֹ�ͷţ����ϴ��ʹ����������˶���1s��ǡ���봫�ʹ����ֹ��١����ʹ�ʼ�����ٶȴ�Сv��ʱ�����У�ľ���봫�ʹ�֮��Ķ�Ħ������Ϊ����0.2��ľ���봫�ʹ�������Ծ�ֹ���Ⱥ����T��5s����v0��10m/s���ٶ��ڴ��ʹ���������Ƴ�������ȫ��ͬ�Ĺ⻬С��С�������m��1kg����1������ľ��������������������в���б�����Ծ�ֹ����2�����������ʱ��t��0.5s��ľ��������ȡg��10m/s2����

��1�����ʹ��˶����ٶȴ�Сv���Լ�ľ�����һ��С��������˲�����߹�ͬ�˶��ٶȴ�Сv1��
��2����1����������ʱ����ľ��������
��3����ľ�����1�������������2���������Ĺ����У�����ľ���봫�ʹ����Ħ����������������
���𰸡���1��v=2m/s ��v1=2m/s��2��t0=1s��3��![]()
��������
��1����ľ���»���������ٶ�Ϊ![]() ����ľ�дӻ����»��Ĺ����ɶ��ܶ�����
����ľ�дӻ����»��Ĺ����ɶ��ܶ�����
![]()
�����⣬ľ�们�ϴ��ʹ����������˶������˶�ѧ��ʽ�У�![]()
�����ڴ�����ţ�ٵڶ������У�![]()
��������������ô��ʹ����ٶ�v=2m/s
���1������ľ�����������ݶ����غ㶨�ɵ�
![]()
�������ݣ����v1=2m/s
��2�����1������ľ�е��������봫�ʹ���˵ľ���Ϊs����1����t0��ľ����������![]()
���1�������ľ�к����߹�ͬ�˶��ļ��ٶ�Ϊa������ţ�ٵڶ�������
![]()
�ã�![]()
��ľ�м����˶���ʱ��Ϊt1,���ٵ��봫�ʹ���ͬ���ٶȵ�ʱ��Ϊt2����
![]() =1s
=1s
��ľ����2s�ڵ�λ��Ϊ��
�����⣺![]()
����t3Ϊľ�лص���1����ײ���������˶���ʱ�䣬���1���2����
![]() �������ݽ�ã�s=10m�� t0=1s
�������ݽ�ã�s=10m�� t0=1s
��3����ľ�����1�������������2������������һ������,���ʹ���λ��Ϊx��ľ�е�λ��Ϊx1,��![]()
![]()
��ľ������봫�ʹ���λ��Ϊ![]()
��ľ���봫�ʹ����Ħ��������������Ϊ![]()

 ��У����ϵ�д�
��У����ϵ�д�