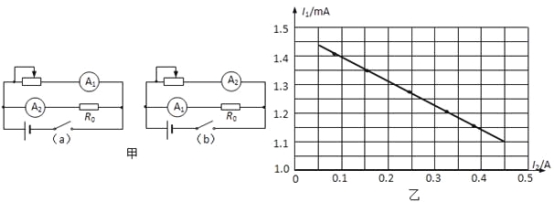
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ®aΘ©Θ§«ψΫ«ΈΣΠ»ΘΫ37ΓψΒΡ–±ΟφΙΧΕ®‘ΎΥ°ΤΫΒΊΟφ…œΓΘΈοΩι‘Ύ”κ–±Οφ≥…ΠΝΘΫ37ΓψΓΔ¥σ–ΓFΘΫ10NΒΡά≠ΝΠΉς”Οœ¬Θ§¥”ΒΉΕΥAΒψ―Ί–±Οφœρ…œΉω‘»Φ”ΥΌ‘ΥΕ·Θ§Ψ≠tΘΫl0sΈοΩι‘ΥΕ·ΒΫBΒψΘ§ΈοΩι‘ΥΕ·ΒΡvΘ≠tΆΦœσ»γΆΦΘ®bΘ©Υυ ΨΓΘ“―÷ΣΈοΩι”κ–±ΟφΦδΒΡΕ·ΡΠ≤Ν“ρ ΐuΘΫ0.5Θ§÷ΊΝΠΦ”ΥΌΕ»gΘΫ10m/s2Θ§sin37ΓψΘΫ0.6Θ§cos37ΓψΘΫ0.8ΓΘœ¬Ν–ΥΒΖ®’ΐ»ΖΒΡ «:
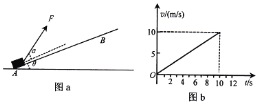
A. ΈοΩιΒΡ÷ ΝΩmΘΫlkg
B. ΈοΩιΒΡΦ”ΥΌΕ»aΘΫlm/s2
C. tΘΫ10s ±ά≠ΝΠΒΡΙΠ¬ PΘΫ80W
D. AΓΔBΝΫΒψΒΡΨύάκxΘΫ100m
ΓΨ¥πΑΗΓΩABC
ΓΨΫβΈωΓΩ
…ηΈοΩι‘ΥΕ·ΒΡΦ”ΥΌΕ»ΈΣaΘ§”…v-tΆΦœσΒΡ–±¬ ±μ ΨΦ”ΥΌΕ»Θ§ΒΟΘΚa=![]() =1m/s2ΘΜ…ηΈοΩιΥυ ήΒΡ÷ß≥÷ΝΠΈΣFNΘ§Υυ ήΒΡΡΠ≤ΝΝΠΈΣFfΘ§ ήΝΠΖ÷Έω»γΆΦΥυ ΨΘ§”…≈ΘΕΌΒΎΕΰΕ®¬…ΒΟΘΚFcosΠΝ-mgsinΠ»-Ff=maΘΜFsinΠΝ+FN-mgcosΠ»=0ΘΜ”÷ Ff=ΠΧFN ΘΜΝΣΝΔ“‘…œ»ΐ ΫΒΟΘΚm=1kgΘ§Ι AB’ΐ»ΖΓΘt=10s ±ΈοΩιΒΡΥΌΕ»ΈΣΘΚv=10m/sΘ§‘ρά≠ΝΠΒΡΙΠ¬ ΈΣΘΚP=FvcosΠΝ=10ΓΝ10ΓΝcos37Γψ W=80WΘ§Ι C’ΐ»ΖΓΘΗυΨίΨίv-tΆΦœσ”κ ±Φδ÷αΥυΈßΒΡΟφΜΐ±μ ΨΈΜ“ΤΘ§ΒΟAΓΔBΝΫΒψΒΡΨύάκΈΣΘΚx=
=1m/s2ΘΜ…ηΈοΩιΥυ ήΒΡ÷ß≥÷ΝΠΈΣFNΘ§Υυ ήΒΡΡΠ≤ΝΝΠΈΣFfΘ§ ήΝΠΖ÷Έω»γΆΦΥυ ΨΘ§”…≈ΘΕΌΒΎΕΰΕ®¬…ΒΟΘΚFcosΠΝ-mgsinΠ»-Ff=maΘΜFsinΠΝ+FN-mgcosΠ»=0ΘΜ”÷ Ff=ΠΧFN ΘΜΝΣΝΔ“‘…œ»ΐ ΫΒΟΘΚm=1kgΘ§Ι AB’ΐ»ΖΓΘt=10s ±ΈοΩιΒΡΥΌΕ»ΈΣΘΚv=10m/sΘ§‘ρά≠ΝΠΒΡΙΠ¬ ΈΣΘΚP=FvcosΠΝ=10ΓΝ10ΓΝcos37Γψ W=80WΘ§Ι C’ΐ»ΖΓΘΗυΨίΨίv-tΆΦœσ”κ ±Φδ÷αΥυΈßΒΡΟφΜΐ±μ ΨΈΜ“ΤΘ§ΒΟAΓΔBΝΫΒψΒΡΨύάκΈΣΘΚx=![]() =50mΘ§Ι D¥μΈσΓΘΙ ―ΓABCΓΘ
=50mΘ§Ι D¥μΈσΓΘΙ ―ΓABCΓΘ

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ