题目内容
13. 如图所示,由于摩擦力的作用,物体A静止在水平面上,这时A受到静摩擦力为f,地面支持力为N.若将A向右稍微移动一点,系统仍保持平衡.则f、N的变化情况是( )
如图所示,由于摩擦力的作用,物体A静止在水平面上,这时A受到静摩擦力为f,地面支持力为N.若将A向右稍微移动一点,系统仍保持平衡.则f、N的变化情况是( )| A. | f增大 | B. | f减小 | C. | N增大 | D. | N减小 |
分析 把A向右移动一些后,物体仍保持静止,所以物体始终处于平衡状态,分别对两物体受力分析应用平衡条件分析即可.
解答 解:设物体的质量为m,物体A的重力为G.
物体始终处于静止状态,所以绳子对物体的拉力T始终等于G,故轻绳的拉力大小不变.
对N受力分析并正交分解如下图所示:
物体仍保持静止,故B受力始终平衡,合力始终为零,由平衡条件得:
N+Tsinθ=G,得 N=G-Gsinθ
f=Tcosθ,得 f=Gcosθ
把A向右移动一些后,θ将变小,由上式可得f增大,N增大.故AC正确,BD错误.
故选:AC
点评 本题为平衡条件得应用:动态分析.常用的方法是画图法和解析式法,一般物体受3个力时常用画图法,受4个以上的力时用解析式法.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
3.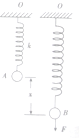 如图所示,轻弹簧的劲度系数为k,下端挂一小球,平衡时小球在A位置,弹簧伸长了x0,现用竖直向下的力F将小球缓慢拉长x至B位置静止,则此拉力F的大小为( )
如图所示,轻弹簧的劲度系数为k,下端挂一小球,平衡时小球在A位置,弹簧伸长了x0,现用竖直向下的力F将小球缓慢拉长x至B位置静止,则此拉力F的大小为( )
 如图所示,轻弹簧的劲度系数为k,下端挂一小球,平衡时小球在A位置,弹簧伸长了x0,现用竖直向下的力F将小球缓慢拉长x至B位置静止,则此拉力F的大小为( )
如图所示,轻弹簧的劲度系数为k,下端挂一小球,平衡时小球在A位置,弹簧伸长了x0,现用竖直向下的力F将小球缓慢拉长x至B位置静止,则此拉力F的大小为( )| A. | kx0 | B. | kx+kx0 | C. | kx-kx0 | D. | kx |
4. 如图所示,某极限运动爱好者(可视为质点)尝试一种特殊的高空运动.他身系一定长度的弹性轻绳,从距水面高度大于弹性轻绳原长的P点以水平初速度v0跳出.他运动到图中a点时弹性轻绳刚好拉直,此时速度与竖直方向的夹角为θ,轻绳与竖直方向的夹角为β,b为运动过程的最低点(图中未画出),在他运动的整个过程中未触及水面,不计空气阻力,重力加速度为g.下列说法正确的是( )
如图所示,某极限运动爱好者(可视为质点)尝试一种特殊的高空运动.他身系一定长度的弹性轻绳,从距水面高度大于弹性轻绳原长的P点以水平初速度v0跳出.他运动到图中a点时弹性轻绳刚好拉直,此时速度与竖直方向的夹角为θ,轻绳与竖直方向的夹角为β,b为运动过程的最低点(图中未画出),在他运动的整个过程中未触及水面,不计空气阻力,重力加速度为g.下列说法正确的是( )
 如图所示,某极限运动爱好者(可视为质点)尝试一种特殊的高空运动.他身系一定长度的弹性轻绳,从距水面高度大于弹性轻绳原长的P点以水平初速度v0跳出.他运动到图中a点时弹性轻绳刚好拉直,此时速度与竖直方向的夹角为θ,轻绳与竖直方向的夹角为β,b为运动过程的最低点(图中未画出),在他运动的整个过程中未触及水面,不计空气阻力,重力加速度为g.下列说法正确的是( )
如图所示,某极限运动爱好者(可视为质点)尝试一种特殊的高空运动.他身系一定长度的弹性轻绳,从距水面高度大于弹性轻绳原长的P点以水平初速度v0跳出.他运动到图中a点时弹性轻绳刚好拉直,此时速度与竖直方向的夹角为θ,轻绳与竖直方向的夹角为β,b为运动过程的最低点(图中未画出),在他运动的整个过程中未触及水面,不计空气阻力,重力加速度为g.下列说法正确的是( )| A. | 极限运动爱好者从P点到b点的运动过程中机械能守恒 | |
| B. | .极限运动爱好者从P点到a点时间的表达式可能为$\frac{{v}_{0}}{gtanθ}$ | |
| C. | .极限运动爰好者到达a点时,tanθ=tanβ | |
| D. | .弹性轻绳原长的表达式可能为:$\frac{{v}_{0}^{2}}{gsinβtanθ}$ |
1.2014年11月25日俄罗斯航天部门用“联盟-FG”运载火箭将载人飞船送往国际空间站,关于这次飞船与火箭上天的情形叙述正确的是( )
| A. | 火箭尾部向外喷气,喷出的气体反过来对火箭产生一个反作用力,从而让火箭获得了向前的推力 | |
| B. | 火箭尾部喷出的气体对空气产生一个作用力,空气的反作用力使火箭获得飞行的动力 | |
| C. | 卫星进入预定轨道之后,与地球之间不存在相互作用 | |
| D. | 火箭飞出大气层后,由于没有了空气,火箭虽然向后喷气,但也无法获得前进的动力 |
8. 如图所示,长为a宽为b的矩形区域内(包括边界)有磁感应强度为B的匀强磁杨,磁场方向垂直纸面向外,O点有一粒子源,某时刻粒子源向磁场所在区域与磁场垂直的平面内所有方向发射大量质量为m电量为q的带正电的粒子,粒子的速度大小相同,粒子在磁场中做匀速圆周运动的周期为T,最先从磁场上边界射出的粒子经历的时间为$\frac{T}{12}$,最后从磁场中飞出的粒子经历的时间为$\frac{T}{4}$,不计重力和粒子之间的相互作用,则( )
如图所示,长为a宽为b的矩形区域内(包括边界)有磁感应强度为B的匀强磁杨,磁场方向垂直纸面向外,O点有一粒子源,某时刻粒子源向磁场所在区域与磁场垂直的平面内所有方向发射大量质量为m电量为q的带正电的粒子,粒子的速度大小相同,粒子在磁场中做匀速圆周运动的周期为T,最先从磁场上边界射出的粒子经历的时间为$\frac{T}{12}$,最后从磁场中飞出的粒子经历的时间为$\frac{T}{4}$,不计重力和粒子之间的相互作用,则( )
 如图所示,长为a宽为b的矩形区域内(包括边界)有磁感应强度为B的匀强磁杨,磁场方向垂直纸面向外,O点有一粒子源,某时刻粒子源向磁场所在区域与磁场垂直的平面内所有方向发射大量质量为m电量为q的带正电的粒子,粒子的速度大小相同,粒子在磁场中做匀速圆周运动的周期为T,最先从磁场上边界射出的粒子经历的时间为$\frac{T}{12}$,最后从磁场中飞出的粒子经历的时间为$\frac{T}{4}$,不计重力和粒子之间的相互作用,则( )
如图所示,长为a宽为b的矩形区域内(包括边界)有磁感应强度为B的匀强磁杨,磁场方向垂直纸面向外,O点有一粒子源,某时刻粒子源向磁场所在区域与磁场垂直的平面内所有方向发射大量质量为m电量为q的带正电的粒子,粒子的速度大小相同,粒子在磁场中做匀速圆周运动的周期为T,最先从磁场上边界射出的粒子经历的时间为$\frac{T}{12}$,最后从磁场中飞出的粒子经历的时间为$\frac{T}{4}$,不计重力和粒子之间的相互作用,则( )| A. | 粒子做圆周运动的半径为2b | |
| B. | 粒子速度大小为$\frac{qBb}{m}$ | |
| C. | a的长度为($\sqrt{3}$+1)b | |
| D. | 最后从磁场中飞出的粒子一定从上边界的中点飞出 |
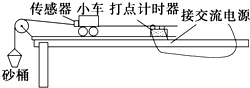 如图所示,为某同学安装的“验证牛顿第二定律”的实验装置,在小车的前端固定一个传感器,和砂桶连接的细线接在传感器上,通过传感器可显示出细线的拉力.在图示状态下开始做实验.
如图所示,为某同学安装的“验证牛顿第二定律”的实验装置,在小车的前端固定一个传感器,和砂桶连接的细线接在传感器上,通过传感器可显示出细线的拉力.在图示状态下开始做实验.
 如图所示,在一条直线上有两个相距0.4m的点电荷A、B,A带电荷量+Q,B带电荷量-9Q,现引入第三个点电荷C,恰好使第三个点电荷处于平衡状态,问:
如图所示,在一条直线上有两个相距0.4m的点电荷A、B,A带电荷量+Q,B带电荷量-9Q,现引入第三个点电荷C,恰好使第三个点电荷处于平衡状态,问: