题目内容
20. 如图所示,在一条直线上有两个相距0.4m的点电荷A、B,A带电荷量+Q,B带电荷量-9Q,现引入第三个点电荷C,恰好使第三个点电荷处于平衡状态,问:
如图所示,在一条直线上有两个相距0.4m的点电荷A、B,A带电荷量+Q,B带电荷量-9Q,现引入第三个点电荷C,恰好使第三个点电荷处于平衡状态,问:(1)若AB固定,则C应带什么性质的电荷?应放于何处?所带电荷量为多少?
(2)若AB不固定,则C应带什么性质的电荷?应放于何处?所带电荷量为多少?
分析 由于QA带正电荷,QB带负电荷,根据同种电荷排斥,异种电荷吸引,要使整个系统处于平衡状态,对其QC受力分析,去判断所处的位置.
解答 解:(1)假设C放在A、B之间,那么A对C的电场力和B对C的电场力方向相同,C不能处于平衡状态,所以假设不成立.
由于B的电量比A大,因此将C放在B的右侧,C不能处于平衡状态,所以假设不成立
故C只能放在A的左侧,设C所在位置与A的距离为r1,C所在位置与B的距离为r2,要使C能处于平衡状态,
所以A对C的电场力大小等于B对C的电场力大小
$\frac{kQq}{{r}_{1}^{2}}=\frac{9kQq}{{r}_{2}^{2}}$
解得r2=3r1
由于A、B固定,从上面的式子可以看出,在上述位置放入第三个点电荷C的电荷量无要求,电性可正可负.
(2)若AB不固定,A、B、C三个电荷要平衡,必须三个电荷的一条直线,外侧二个电荷相互排斥,中间电荷吸引外侧两个电荷,所以外侧两个电荷距离大,要平衡中间电荷的拉力,必须外侧电荷电量大,中间电荷电量小,所以C必须为负电,在A的左侧.
设C所在位置与A的距离为r,则C所在位置与B的距离为L+r,要能处于平衡状态,
所以A对C的电场力大小等于B对C的电场力大小,设C的电量为q则有
$\frac{kQq}{{r}^{2}}=\frac{9kQq}{(r+L)^{2}}$
解得r=0.2m
对点电荷A,其受力也平衡,则$\frac{kQq}{{r}^{2}}=\frac{9k{Q}^{2}}{{L}^{2}}$
解得$q=\frac{9Q}{4}$;
答:(1)若AB固定,则C应带正负电荷均可,应放于A左侧距离B的距离等于距离A的3倍距离处,所带电荷量无要求;
(2)若AB不固定,则C应带负电荷,应放于A左侧0.2m处,所带电荷量为$\frac{9Q}{4}$.
点评 本题考查了库仑定律和共点力平衡,若A、B固定,对第三个电荷的电量和电性无要求.若三个电荷均处于自由状态,则可以可记住口诀:两同夹异、两大夹小、近小远大.

 如图所示,由于摩擦力的作用,物体A静止在水平面上,这时A受到静摩擦力为f,地面支持力为N.若将A向右稍微移动一点,系统仍保持平衡.则f、N的变化情况是( )
如图所示,由于摩擦力的作用,物体A静止在水平面上,这时A受到静摩擦力为f,地面支持力为N.若将A向右稍微移动一点,系统仍保持平衡.则f、N的变化情况是( )| A. | f增大 | B. | f减小 | C. | N增大 | D. | N减小 |
| A. | 10N | B. | 40N | C. | 70N | D. | 100N |
 我国正在进行的探月工程是高新技术领域的一次重大科技活动,在探月工程中飞行器成功变轨至关重要.如图所示,假设月球半径为R,月球表面的重力加速度为g0,飞行器在距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )
我国正在进行的探月工程是高新技术领域的一次重大科技活动,在探月工程中飞行器成功变轨至关重要.如图所示,假设月球半径为R,月球表面的重力加速度为g0,飞行器在距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )| A. | 飞行器在B点处点火后,动能增加 | |
| B. | 由已知条件不能求出飞行器在Ⅱ轨道上运行周期 | |
| C. | 只有万有引力作用下,飞行器在轨道Ⅱ上通过B点的加速度大于在轨道Ⅲ在B点的加速度 | |
| D. | 飞行器在轨道Ⅲ绕月球运行一周所需的时间为2π$\sqrt{\frac{R}{{g}_{0}}}$ |
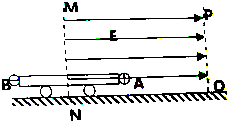 如图所示,长为2L的平板绝缘小车放在光滑水平面上,小车两端固定两个绝缘的带电小球A和B,A、B所带电荷量分别为+2q和-3q,小车(包括带电小球A、B)的总质量为m,虚线MN与PQ均沿竖直方向且相距3L,开始时虚线MN位于小车正中间,若视带电小球为质点,在虚线MN、PQ间加上方向水平向右、场强大小为E的匀强电场后,小车开始运动,
如图所示,长为2L的平板绝缘小车放在光滑水平面上,小车两端固定两个绝缘的带电小球A和B,A、B所带电荷量分别为+2q和-3q,小车(包括带电小球A、B)的总质量为m,虚线MN与PQ均沿竖直方向且相距3L,开始时虚线MN位于小车正中间,若视带电小球为质点,在虚线MN、PQ间加上方向水平向右、场强大小为E的匀强电场后,小车开始运动, 在光滑水平面上固定一个内壁光滑的竖直圆筒S(如图为俯视图),圆筒半径为R=0.5m.一根长r=0.4m的绝缘细线一端固定于圆筒圆心O点,另一端系住一个质量为m=0.2kg、带电量为q=+5×10-5C的小球.空间有一场强为E=4×104N/C的匀强电场,电场方向与水平面平行.将细线拉至与电场线平行,给小球大小为v0=10m/s、方向垂直于电场线的初速度.
在光滑水平面上固定一个内壁光滑的竖直圆筒S(如图为俯视图),圆筒半径为R=0.5m.一根长r=0.4m的绝缘细线一端固定于圆筒圆心O点,另一端系住一个质量为m=0.2kg、带电量为q=+5×10-5C的小球.空间有一场强为E=4×104N/C的匀强电场,电场方向与水平面平行.将细线拉至与电场线平行,给小球大小为v0=10m/s、方向垂直于电场线的初速度.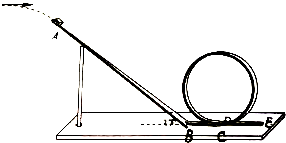 为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的.其中AB与BC轨道以微小圆弧相接,如图所示.一个质量m=1kg小物块以初速度v0=4.0m/s,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数μ=0.5(g取10m/s2,sin37°=0.6,cos37°=0.8)
为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的.其中AB与BC轨道以微小圆弧相接,如图所示.一个质量m=1kg小物块以初速度v0=4.0m/s,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下.已知物块与倾斜轨道的动摩擦因数μ=0.5(g取10m/s2,sin37°=0.6,cos37°=0.8)