题目内容
12．
质量M=4kg，m=2kg的物体如图所示，M与地面的摩擦力不计，m与M的摩擦因数为0.1，现在有一个力F分别两次作用在M和m上，至少为多大，M和m发生相对运动（ ）| A． | 2N 6N | B． | 3N 2N | C． | 3N 6N | D． | 6N 3N |
分析 当m与M的静摩擦力达到最大值时两者刚要发生相对滑动，分别隔离m和M分析，求出最大加速度，再对整体，结合牛顿第二定律求出最小拉力．
解答 解：当力F作用在M上时，若M和m刚要发生相对运动，则两者之间的静摩擦力达到最大值．
根据牛顿第二定律，对m有：μmg=ma，得：a=μg=1m/s2．
对整体有：F=（M+m）a=（4+2）×1N=6N．
同理，当力F作用在m上时，若M和m刚要发生相对运动，则两者之间的静摩擦力达到最大值．
根据牛顿第二定律对M有：μmg=Ma，得：a=0.5m/s2．
对整体有：F=（M+m）a=（4+2）×0.5N=3N．
故D正确，ABC错误
故选：D
点评 解决本题的关键是要明确两个刚要发生相对滑动时静摩擦力达到最大值，要灵活选择研究对象，运用隔离法和整体法结合进行研究．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．如图所示，A、B两物体中间连接一压缩弹簧，且用细线拴住，静止放在光滑水平地面上，C物体与B靠在一起，烧断细线，下列说法正确的是（ ）
| A． | 弹簧拉伸至最长时，A、B两物体和弹簧组成的系统总动量为0 | |
| B． | 弹簧拉伸至最长时，弹簧的弹性势能与初始时相同 | |
| C． | 弹簧拉伸至最长时，弹簧的弹性势能小于初始时的弹性势能 | |
| D． | 弹簧拉伸至最长时，A、B、C和弹簧组成的系统总动量不为0 |
2．物体做匀加速直线运动，已知它在第1s末的速度是6m/s，在第2s末的速度是8m/s，则下面结论正确的是（ ）
| A． | 物体零时刻速度是3m/s | |
| B． | 物体的加速度是2m/s2 | |
| C． | 任何1s内的速度变化都是2m/s | |
| D． | 每1s初的速度比前1s末的速度大2m/s |
7．
如图，一轻弹簧一端固定在墙角上，另一端自由，整个弹簧放在水平粗糙地面上，现用一木块向右将弹簧压缩一段距离后释放，则从刚释放一直到木块刚脱离弹簧的过程中，有关木块的运动下列说法正确的是（ ）
如图，一轻弹簧一端固定在墙角上，另一端自由，整个弹簧放在水平粗糙地面上，现用一木块向右将弹簧压缩一段距离后释放，则从刚释放一直到木块刚脱离弹簧的过程中，有关木块的运动下列说法正确的是（ ）| A． | 加速度先变小后变大 | B． | 加速度一直变小 | ||
| C． | 速度先变大后变小 | D． | 速度一直变大 |
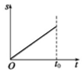
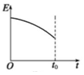
17．如图（a）所示，固定斜面AB与水平面BC在B处用小圆弧连接，可看成质点的物块在t=0时刻从斜面的A点沿斜面下滑，经过B点进入水平面，最后停在水平面的C点，设其经过B点时没有机械能的损耗，其运动的速率-时间图象如图（b）所示．若物块与各接触面间的动摩擦因数相同，重力加速度g及图中的v1、t1均为已知量，则可求出（ ）
| A． | 物块的质量 | B． | 斜面的倾角 | ||
| C． | 物块与接触面的动摩擦因数 | D． | AC两点间的距离 |
4．
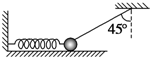在动摩擦因数μ=0.3的水平面上有一个质量为m=1kg的小球，小球与竖直方向成θ=45°角的不可伸长的轻绳一端相连，如图所示．此时小球处于静止平衡状态，且水平面对小球的弹力恰好为零，当剪断轻绳的瞬间，小球的加速度的大小为（取g=10m/s2）（ ）
在动摩擦因数μ=0.3的水平面上有一个质量为m=1kg的小球，小球与竖直方向成θ=45°角的不可伸长的轻绳一端相连，如图所示．此时小球处于静止平衡状态，且水平面对小球的弹力恰好为零，当剪断轻绳的瞬间，小球的加速度的大小为（取g=10m/s2）（ ）| A． | 0 | B． | 10 m/s2 | C． | 7 m/s2 | D． | $10\sqrt{2}$m/s2 |
