题目内容
17.如图(a)所示,固定斜面AB与水平面BC在B处用小圆弧连接,可看成质点的物块在t=0时刻从斜面的A点沿斜面下滑,经过B点进入水平面,最后停在水平面的C点,设其经过B点时没有机械能的损耗,其运动的速率-时间图象如图(b)所示.若物块与各接触面间的动摩擦因数相同,重力加速度g及图中的v1、t1均为已知量,则可求出( )
| A. | 物块的质量 | B. | 斜面的倾角 | ||
| C. | 物块与接触面的动摩擦因数 | D. | AC两点间的距离 |
分析 根据v-t图象的斜率求出两段时间内物块的加速度大小,根据牛顿第二定律列式,可求得斜面的倾角和动摩擦因数.由图象的“面积”求得AB和BC的长度,结合斜面的倾角可求得AC间的距离.
解答 解:A、设物块在AB段和BC段运动的加速度大小分别为a1和a2.
根据v-t图象的斜率表示加速度,可得 a1=$\frac{{v}_{1}}{{t}_{1}}$,a2=$\frac{{v}_{1}}{2{t}_{1}}$
根据牛顿第二定律得:
AB有:mgsinα-μmgcosα=ma1.
BC有:μmg=ma2,得 μ=$\frac{{a}_{2}}{g}$
由上可知,能求出物块与接触面的动摩擦因数μ,也能解出斜面的倾角α,但不能解不出物块的质量m.
根据v-t图象与时间轴所围的面积表示位移,可以求出AB和BC的长度,则AC两点间的距离 AC=ABcosα+BC,可知可以求出AC两点间的距离.故A错误,BCD正确.
故选:BCD
点评 解决本题的关键要读懂图象的物理意义,知道v-t图象的斜率等于加速度,面积表示位移,分段半定量研究.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
6.下列说法正确的是( )
| A. | 卢瑟福通过α粒子散射实验确定了原子核是由质子和中子组成的 | |
| B. | 康普顿效应证实了光的粒子特性 | |
| C. | 一群处于第四能级的氢原子向基态跃迁时,将向外辐射六种不同频率的光子 | |
| D. | 爱因斯坦质能方程E=mc2表明,物体具有的能量和它的质量之间有简单的正比关系 |
7.如图a所示,质量为1 kg的物体在水平力F作用下,沿水平方向做直线运动,拉力F与位移s的关系如图b所示,前5m位移内物体做匀速直线运动,则在物体发生10m位移的过程中( )


| A. | 重力做功为WG=100J | B. | 拉力F做功为WF=150J | ||
| C. | 所有力做的总功W总=50J | D. | 摩擦阻力做功为Wf=0J |
5.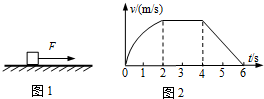 如图1所示,在粗糙程度处处相同的水平地面上,物块在水平向右的力F作用下由静止开始运动.运动的速度v与时间t的关系如图2所示.由图象可知,( )
如图1所示,在粗糙程度处处相同的水平地面上,物块在水平向右的力F作用下由静止开始运动.运动的速度v与时间t的关系如图2所示.由图象可知,( )
 如图1所示,在粗糙程度处处相同的水平地面上,物块在水平向右的力F作用下由静止开始运动.运动的速度v与时间t的关系如图2所示.由图象可知,( )
如图1所示,在粗糙程度处处相同的水平地面上,物块在水平向右的力F作用下由静止开始运动.运动的速度v与时间t的关系如图2所示.由图象可知,( )| A. | 在2s-4s内,力F=0 | B. | 在4s-6s内,力F可能为零 | ||
| C. | 在0-2s内,力F逐渐变小 | D. | 在0-2s内,力F逐渐增大 |
12. 质量M=4kg,m=2kg的物体如图所示,M与地面的摩擦力不计,m与M的摩擦因数为0.1,现在有一个力F分别两次作用在M和m上,至少为多大,M和m发生相对运动( )
质量M=4kg,m=2kg的物体如图所示,M与地面的摩擦力不计,m与M的摩擦因数为0.1,现在有一个力F分别两次作用在M和m上,至少为多大,M和m发生相对运动( )
 质量M=4kg,m=2kg的物体如图所示,M与地面的摩擦力不计,m与M的摩擦因数为0.1,现在有一个力F分别两次作用在M和m上,至少为多大,M和m发生相对运动( )
质量M=4kg,m=2kg的物体如图所示,M与地面的摩擦力不计,m与M的摩擦因数为0.1,现在有一个力F分别两次作用在M和m上,至少为多大,M和m发生相对运动( )| A. | 2N 6N | B. | 3N 2N | C. | 3N 6N | D. | 6N 3N |
6.如图所示为某一电源的U-I曲线,由图可知( )
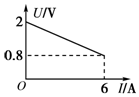

| A. | 电源电动势为2.0 V | |
| B. | 电源内电阻为$\frac{1}{3}$Ω | |
| C. | 电源短路时电流为10A | |
| D. | 电路路端电压为1.5 V时,电路中电流为5.0 A |
7.历史上有些科学家曾这样定义直线运动的加速度:A=$\frac{{v}_{x}-{v}_{0}}{x}$,其中v0和vx分别表示某段位移x内的初速度和末速度.而现在物理学中加速度的定义式为a=$\frac{{v}_{t}-{v}_{0}}{t}$,下列说法正确的是( )
| A. | 对于加速直线运动,即初速度和加速度方向相同,若a不变,则A将变小 | |
| B. | 对于加速直线运动,即初速度和加速度方向相同,若A不变,则a将变小 | |
| C. | 若A不变,则物体在中间时刻的速度为$\frac{{v}_{0}+{v}_{x}}{2}$ | |
| D. | 若A不变,则物体在中间位置处的瞬时速度将小于物体中间时刻的瞬时速度 |
 一辆总质量为20t的卡车在下坡时,司机突然发现刹车失灵,同时发动机又失去动力,此时速度表的示数为54km/h,卡车继续沿坡匀加速直行200m、下降高度50m后,刚好进入一条避险车道(如图所示),此时速度表的示数为90km/h.已知卡车在下坡过程中所受阻力恒定,g取10m/s2.
一辆总质量为20t的卡车在下坡时,司机突然发现刹车失灵,同时发动机又失去动力,此时速度表的示数为54km/h,卡车继续沿坡匀加速直行200m、下降高度50m后,刚好进入一条避险车道(如图所示),此时速度表的示数为90km/h.已知卡车在下坡过程中所受阻力恒定,g取10m/s2.