题目内容
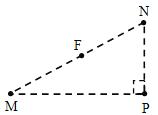
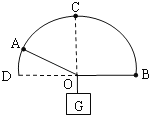
【题目】如图所示,在水平边界MN上方有磁感应强度大小为B0、方向垂直纸面向外的匀强磁场,磁感应强度为B,O、A是MN上的两点,OA距离为L,PQ是一足够长的挡板,粒子打在挡板上均被吸收,开始时P点与O点重合,∠QON=θ=53°。在OA之间有大量质量为m、电荷量为﹢q且速度相同的粒子,速度方向均垂直边界MN竖直向上,且在纸面内。其中从OA中点射入的粒子,恰能垂直打在挡板上(不计粒子重力及其相互作用)

(1)求粒子的初速度大小v0;
(2)求挡板上被粒子打中的长度x1;
(3)若将挡板沿MN向右平移![]() L距离,方向不变;磁感应强度的大小变为原来的一半,求挡板上被粒子打中的长度x2。
L距离,方向不变;磁感应强度的大小变为原来的一半,求挡板上被粒子打中的长度x2。
【答案】(1) v0=![]() (2) x1=d1=
(2) x1=d1=![]() L (3) x2=
L (3) x2=![]() L
L
【解析】(1)粒子运动轨迹的圆心为O点,轨迹如图1所示。
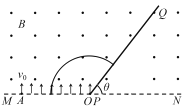
设粒子轨迹的半径为r1,由几何关系得:
![]()
由洛伦兹力提供向心力:
![]()
解得:![]()
(2)(i)如图2所示,
从某点射出的粒子水平打在板上,其轨迹圆圆心为O1,则此粒子打在板上的点离P点最远,最远距离设为d1,由几何关系得最远距离:
![]()
该粒子入射点在O点左侧距O点的距离为![]()
是存在的,符合题意;
(ii)如图2所示,从A点射入的粒子打在板上的O(P)点,该粒子轨迹圆圆心O2;
(iii)如图3所示,从O点发出的粒子打在板上的点离P点的距离为d2,其轨迹圆圆心为O3,由几何关系得最近距离
![]() ,不是最远距离
,不是最远距离
综上所述,挡板上被粒子打中的长度
![]() ;
;
(3)磁感应强度的大小变为原来的一半,设粒子在磁场中运动的轨迹半径为r2,由洛伦兹力提供向心力
![]()
解得:![]()
所有粒子的轨迹圆心在O点右侧长度L的范围内。
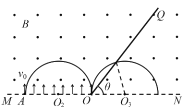
(i)如图4所示,

从某点射出的粒子水平打在板上,其轨迹圆圆心为O4,则此粒子打在板上的点离P点最远,最远距离设为d4,由几何关系得最远距离:
![]()
该粒子入射点离O4点的距离为L,而OO4的距离为![]() ,即该粒子是不存在的;
,即该粒子是不存在的;
(ii)从O点射入的粒子打在挡板上的点离P点最远,该粒子轨迹如图所示,其轨迹圆圆心为O5,最远距离设为d5,由几何关系得:
![]()
解得:![]()
(iii)从A点射入的粒子打在挡板上的点离P点最远,该粒子轨迹如图所示,

其轨迹圆圆心恰好为O,最远距离设为d6,由几何关系得:
![]()
解得:![]()
综上所述,挡板上被粒子打中的长度
![]() 。
。