题目内容
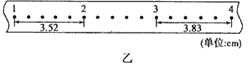
【题目】在研究匀变速直线运动的实验中得到一条如图所示纸带，已知相邻计数点的时间间隔为0.1s，x1=3.50cm，x2=5.30cm，
（1）请计算打计数点1时纸带的速度填入表格________
算出小车经过各计数点瞬时速度如下：
计数点序号 | 1 | 2 | 3 | 4 | 5 | 6 |
计数点对应的时刻（s） | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
通过计数点的速度（m/s） | 0.62 | 0.81 | 1.00 | 1.15 | 1.34 |
（2）为了计算加速度，合理的方法是：___________
A.根据任意两计数点的速度用公式算出加速度
B.根据实验数据画出v－t图，量出其倾角θ，由公式a = tanθ求出加速度
C.根据实验数据画出v－t图，由图线上相距较远的两点所对应的速度、时间，用公式
算出加速度
D.依次算出通过连续两计数点间的加速度，算出平均值作为小车的加速度
【答案】
C
【解析】
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上某点时小车的瞬时速度大小。根据各计数点的瞬时速度作出速度-时间图象，解出其斜率即是小车的加速度．图象法能有效地舍弃误差较大的数据，减小偶然误差。
（1）根据匀变速直线运动中时间中点的速度等于该过程中的平均速度得：
。
（2）在处理实验数据时，如果只使用其中两个数据，由于偶然误差的存在可能会造成最后误差较大；所以我们可以根据实验数据画出v-t图象，考虑到误差，不可能是所有点都整齐的排成一条直线，连线时，应该尽量使那些不能画在线上的点均匀地分布在线的两侧，这样图线上会舍弃误差较大的点，由图线上任意两点所对应的速度及时间，用公式
算出加速度，所以误差小，故A错误，C正确；根据实验数据画出v-t图象，当纵坐标取不同的标度时，图象的倾角就会不同，所以量出其倾角，用公式a=tanα算出的数值并不是加速度，故B错误；这种方法是不对的，因为根本就不知道加速度是一个什么函数，如果是一个变化值这种方法完全是错误的，除非你能确定加速度是什么函数，故D错误。所以C正确，ABD错误。
