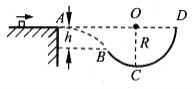
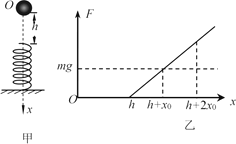
题目内容
【题目】如图所示，一个质量m=1kg的物块，在F=5N的拉力作用下，从静止开始沿水平面做匀加速直线运动，拉力方向与水平方向成θ=37°。假设物块与水平面之间的滑动摩擦因数μ=0.5，取重力加速度g=10m/s2。sin37°=0. 6，cos37°=0. 8。
(1)画出物块的受力示意图；
(2)求物块运动的加速度大小；
(3)求物块移动的位移达到16m时的速度大小。
【答案】(1)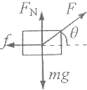
(2)a=1m/s2 (3)
【解析】
(1)对物块受力分析，受重力、拉力、支持力和滑动摩擦力，再画出物块的受力示意图；
(2)根据牛顿第二定律求出物体的加速度的大小；
(3)物体做匀加速直线运动，由v2=2ax可以求得物体的速度大小．
(1)物块受到重力、拉力、支持力和滑动摩擦力，物块的受力示意图如下:
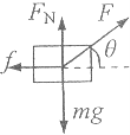
(2)物块竖直方向受力平衡，则有：Fsin37°+FN=mg
此物块所受到的滑动摩擦力为：f=μFN=μ(mg-Fsin37°)
代入数据解得：f=3N
根据牛顿第二定律，有：Fcos37°-f=ma
代入数据解得：a=1m/s2
(3)根据匀变速直线运动规律v2=2ax
代入数据得:
智趣寒假作业云南科技出版社系列答案
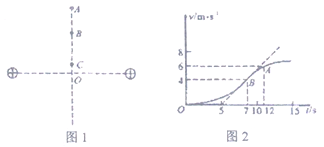
【题目】在研究匀变速直线运动的实验中得到一条如图所示纸带，已知相邻计数点的时间间隔为0.1s，x1=3.50cm，x2=5.30cm，
（1）请计算打计数点1时纸带的速度填入表格________
算出小车经过各计数点瞬时速度如下：
计数点序号 | 1 | 2 | 3 | 4 | 5 | 6 |
计数点对应的时刻（s） | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
通过计数点的速度（m/s） | 0.62 | 0.81 | 1.00 | 1.15 | 1.34 |
（2）为了计算加速度，合理的方法是：___________
A.根据任意两计数点的速度用公式算出加速度
B.根据实验数据画出v－t图，量出其倾角θ，由公式a = tanθ求出加速度
C.根据实验数据画出v－t图，由图线上相距较远的两点所对应的速度、时间，用公式
算出加速度
D.依次算出通过连续两计数点间的加速度，算出平均值作为小车的加速度
