题目内容
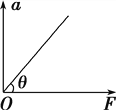
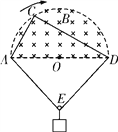
【题目】光滑水平地面上固定着一带滑轮的竖直硬杆,一根轻绳的一端系着小滑块,另一端绕过滑轮,如图所示,现用恒力![]() 水平向左拉小滑块的同时,用恒力
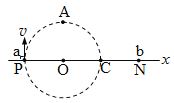
水平向左拉小滑块的同时,用恒力![]() 拉绳子的另一端,使滑块从A点由静止开始沿地面向右运动,已知B和C是A点右方的两点,且AB=2BC,小滑块到达A点时绳子与水平方向的夹角为30°,小滑块到达B点时绳子与水平方向的夹角为45°,不计滑轮大小以及绳子与滑轮的摩擦,则以下说法正确的是( )
拉绳子的另一端,使滑块从A点由静止开始沿地面向右运动,已知B和C是A点右方的两点,且AB=2BC,小滑块到达A点时绳子与水平方向的夹角为30°,小滑块到达B点时绳子与水平方向的夹角为45°,不计滑轮大小以及绳子与滑轮的摩擦,则以下说法正确的是( )

A. 滑块从A点运动到C点加速度先变小再变大
B. 滑块从A点运动到B点恒力![]() 做的功是从B点运动到C点做的功的2倍
做的功是从B点运动到C点做的功的2倍
C. 滑块从A点到C点克服恒力![]() 做功的功率先增大后减小
做功的功率先增大后减小
D. 若定滑轮的高度为H,物块到达B点时动能为![]()
【答案】ACD
【解析】在B点,对滑块由牛顿第二定律得: ![]() ,而
,而![]() ,解得:
,解得: ![]() ,故从A到B,
,故从A到B, ![]() 从
从![]() 增大到
增大到![]() ,故
,故![]() 减小,最终
减小,最终![]() ,由牛顿第二定律:
,由牛顿第二定律: ![]() ,可知从A到B,
,可知从A到B, ![]() 不断减小;从B到C,
不断减小;从B到C, ![]() 从
从![]() 继续增大,故
继续增大,故![]() 减小,此时
减小,此时![]() ,由牛顿第二定律:
,由牛顿第二定律: ![]() ,可知从A到B,
,可知从A到B, ![]() 不断增大,故A正确;从A到B,
不断增大,故A正确;从A到B, ![]() 做的功为
做的功为![]() ,从B到C,
,从B到C, ![]() 做的功为
做的功为![]() ,由题知
,由题知![]() ,但
,但![]() 与
与![]() 不相等,是不断变化的,故从A到B恒力
不相等,是不断变化的,故从A到B恒力![]() 做的功不是从B到C做的功的2倍,故B错误;由A项分析知,加速度先正方向减小再反向增大,故速度先增大后减小,根据
做的功不是从B到C做的功的2倍,故B错误;由A项分析知,加速度先正方向减小再反向增大,故速度先增大后减小,根据![]() ,可知
,可知![]() 瞬时功率先增大后减小,故C正确;在A点,绳子的长度为
瞬时功率先增大后减小,故C正确;在A点,绳子的长度为![]() ,A到滑轮的水平距离
,A到滑轮的水平距离![]() ,在B点,绳子的长度为
,在B点,绳子的长度为![]() ,B到滑轮的水平距离
,B到滑轮的水平距离![]() ,故沿
,故沿![]() 方向的位移为
方向的位移为![]() ,则
,则![]() 做的功为
做的功为![]() ,滑块的位移为
,滑块的位移为![]() ,则
,则![]() 做的功为
做的功为![]() ,根据动能定理得:
,根据动能定理得: ![]() ,联立解得:
,联立解得: ![]() ,故D正确;故选ACD.
,故D正确;故选ACD.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目