Question

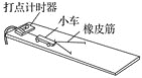
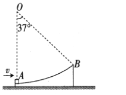
【题目】如图所示，整个空间存在水平向右的匀强电场E=1.0×103N/C，半径为R=0.2m的光滑半圆形细管MPN固定在竖直平面内，管口M、N的连线水平，在细管右侧某处有一光滑绝缘的水平轨道CD，轨道左端C处静止放置一个绝缘不带电、质量mB=1.0kg的小球B，轨道右侧足够长．现将质量为mA=1.0kg、电量q=5.0×10-3C的带正电小球A从管口M（小球直径略小于细管直径）静止释放，从管口N离开细管之后恰能沿水平方向从C点进入轨道CD，与小球B发生弹性碰撞（碰撞过程无电荷转移、无机械能损失），两小球均可视为质点，在以后运动过程中两小球始终在水平轨道上，重力加速度g=10m/s2．求：

（1）小球经过细管最低点P时对细管的压力；

（2）第一次弹性碰撞前的瞬间小球A的速度vA0大小；

（3）设小球A、B在C点右侧K处（图中未画出）发生第16次碰撞，求CK的距离．

Answer 1

【答案】(1) 160N，竖直向下 (2) 1 m/s (3) 48m

【解析】

(1)A球A→P，由动能定理得

A球在P点，牛顿第二定律得

解得

=40N

牛顿第三定律得细管受到的压力

=160N

方向竖直向下

(2)A球M→N，由动能定理得

解得

m/s

A球N→C，做斜上抛运动，则竖直方向：

=0.2s

水平方向

=5m/s2

第一次碰撞前A球速度为

=1m/s

(3)取水平向右为正方向，对A、B球第1次弹性碰撞，有

解得

vA1=0， vB1=1 m/s

设第1、2次碰撞的时间间隔为t1，第1次碰撞后A球初速度vA1=0、做加速度a=5m/s2的匀加速直线，B球以vB1=1 m/s做匀速直线运动，则有

\

解得

=0.4s

设第2次碰撞前A、B球速度分别为、，则

=2m/s

=1m/s

对A、B球第2次弹性碰撞，有

解得

vA2=1 m/s， vB2=2m/s

设第2、3次碰撞的时间间隔为t2，则有

解得

=0.4s

可得第3次碰撞前瞬间A、B球速度分别为=3m/s ， = vB2=2m/s同理，

对第3次弹性碰撞，碰撞后瞬间A、B球速度分别为

vA3=2m/s，vB3=3m/s

故每相邻两次碰撞后B球速度是等差数列，公差为d=1m/s，第15次碰撞后vB15=15m/s，每相邻两次碰撞的时间间隔相等t=0.4s

综上，CK距离

S==48m