题目内容
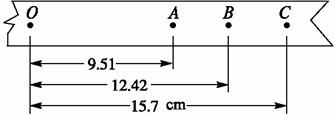
在用自由落体运动验证机械能守恒定律的实验中,已知打点计时器打点时间间隔为T,查得当地重力加速度g,测出所用重物的质量m,实验中得到一条点迹清晰的纸带,O为重物开始下落时记录的点,另选连续的4个点A、B、C、D作为测量点,经测量知道A、B、C、三点到D点的距离分别为x1、x2、x3,根据以上数据可知,打点计时器打C点时重物的动能为
,从A点到C点重物的重力势能的减少量为

m
| ||
| 8T2 |
m
| ||
| 8T2 |
mg(x1-x3)
mg(x1-x3)
.(用m、g、x1、x2、x3等量表示) 
分析:纸带实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度.从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.
解答:解:匀变速直线运动中,时间中点的瞬时速度等于该过程中的平均速度,因此有:
vC=
打点计时器打C点时重物的动能为:
Ek=
m
=
重力势能减小量为:
△Ep=mgh=mg(x1-x3)
故答案为:
,mg(x1-x3).
vC=
| x2 |
| 2T |
打点计时器打C点时重物的动能为:
Ek=
| 1 |
| 2 |
| v | 2 C |
m
| ||
| 8T2 |
重力势能减小量为:
△Ep=mgh=mg(x1-x3)
故答案为:
m
| ||
| 8T2 |
点评:运用运动学公式和动能、重力势能的定义式解决问题是该实验的常规问题,同时要熟练应用基本物理规律解决实验问题.

练习册系列答案
相关题目