题目内容
8. 如图所示xOy平面内,在x轴上从电离室产生的带正电的粒子,以几乎为零的初速度飘入电势差为U=200V的加速电场中,然后经过右侧极板上的小孔沿x轴进入到另一匀强电场区域,该电场区域范围为-l≤x≤0(l=4cm),电场强度大小为E=$\sqrt{3}$×104V/m,方向沿y轴正方向.带电粒子经过y轴后,将进入一与y轴相切的圆形边界匀强磁场区域,磁场区域圆半径为r=2cm,圆心C到x轴的距离为d=4$\sqrt{3}$cm,磁场磁感应强度为B=8×10-2T,方向垂直xoy平面向外.带电粒子最终垂直打在与y轴平行、到y轴距离为L=6cm的接收屏上.求:
如图所示xOy平面内,在x轴上从电离室产生的带正电的粒子,以几乎为零的初速度飘入电势差为U=200V的加速电场中,然后经过右侧极板上的小孔沿x轴进入到另一匀强电场区域,该电场区域范围为-l≤x≤0(l=4cm),电场强度大小为E=$\sqrt{3}$×104V/m,方向沿y轴正方向.带电粒子经过y轴后,将进入一与y轴相切的圆形边界匀强磁场区域,磁场区域圆半径为r=2cm,圆心C到x轴的距离为d=4$\sqrt{3}$cm,磁场磁感应强度为B=8×10-2T,方向垂直xoy平面向外.带电粒子最终垂直打在与y轴平行、到y轴距离为L=6cm的接收屏上.求:(1)带电粒子通过y轴时离x轴的距离;
(2)带电粒子的比荷;
(3)若另一种带电粒子从电离室产生后,最终打在接收屏上y=$\frac{8}{3}$$\sqrt{3}$cm处,则该粒子的比荷又是多少?
分析 (1)带电粒子在电场中做为类平抛运动,由运动的合成和分解规律可求得偏转位移;
(2)根据粒子在电场中的运动明确粒子进入磁场时的速度大小及方向,再由洛仑兹力充当向心力可明确比荷;
(3)由题意明确半径及运动图象,再由洛仑兹力充当向心力可求得比荷.
解答 解:(1)带电粒子在加速电场中被加速 qU=$\frac{1}{2}$mv02
通过沿y轴正方向的电场中时,在x方向上做匀速运动l=v0t
在y方向做初速度为零的匀加速运动,加速度为a=$\frac{Eq}{m}$
在y方向的位移为 y1=$\frac{1}{2}$at2
由以上各式解得 y1=$\frac{E{l}^{2}}{4U}$
代入数据得 y1=2$\sqrt{3}$×10-2m
(2)由(1)中公式可得 v0=$\sqrt{\frac{2qU}{m}}$
带电粒子通过y轴时沿y轴方向的速度为vy=at
如图所示,速度方向满足 tanα=$\frac{{v}_{y}}{{v}_{0}}$
由以上各式解得 tanα=$\frac{El}{2U}$
代入数据得 tanα=$\sqrt{3}$
则可知α=60°
带电粒子通过y轴时的速度大小为v=$\frac{{v}_{0}}{cosα}$=2v0
由 tan∠PCA=$\frac{d-{y}_{1}}{r}$=$\sqrt{3}$;
可得:∠PCA=60°
可见,带电粒子通过y轴时的速度方向指向C点.
所以带电粒子在磁场中做匀速圆周运动时,转过的圆心角为α=60°.
带电粒子圆周运动的半径为
R=rcot$\frac{α}{2}$=$\sqrt{3}$r=2$\sqrt{3}$×10-2
洛伦兹力提供向心力 qvB=m$\frac{{v}^{2}}{R}$
解得$\frac{q}{m}$=$\frac{8U}{{B}^{2}{R}^{2}}$=$\frac{8U}{3{B}^{2}{r}^{3}}$
代入数据得$\frac{q}{m}$=$\frac{1}{3}$×108C/kg 
(3)由(1)(2)知,带电粒子经过y轴时的位置和速度方向与比荷无关,所以另一种带电粒子也将以指向C点的方向进入到匀强磁场区域.轨迹如图所示.
粒子从磁场中射出时的速度方向满足tan∠NCM=$\frac{d-y}{r}$=$\frac{\sqrt{3}}{3}$
可得∠NCM=30°
此带电粒子在磁场中转过的角度为α′=60°+30°=90°
其圆周运动的半径为R′=r
同理有 $\frac{q′}{m′}$=$\frac{8U}{{B}^{2}R{′}^{2}}$=$\frac{8U}{{B}^{2}{r}^{2}}$
代入数据得$\frac{q′}{m′}$=1×108C/kg
解:(1)带电粒子通过y轴时离x轴的距离2$\sqrt{3}$×10-2m;
(2)带电粒子的比荷$\frac{1}{3}$×108C/kg
(3)若另一种带电粒子从电离室产生后,最终打在接收屏上y=$\frac{8}{3}$$\sqrt{3}$cm处,则该粒子的比荷1×108C/kg
点评 本题考查带电粒子在电场和磁场中的运动情况,要注意明确粒子的运动轨迹;明确带电粒子在电场中采用运动的合成与分解求解;而在磁场中要注意明确圆周运动的规律应用,注意几何关系及洛仑兹力与向心力的关系.

 阅读快车系列答案
阅读快车系列答案 如图所示,A、B、C三个物块重力均为100N,小球P的重力为20N,作用在物块B上的水平向左的拉力F=30N,整个系统静止,与物块C相连的轻绳恰好水平,下列说法正确的是( )
如图所示,A、B、C三个物块重力均为100N,小球P的重力为20N,作用在物块B上的水平向左的拉力F=30N,整个系统静止,与物块C相连的轻绳恰好水平,下列说法正确的是( )| A. | A和B之间的摩擦力为30N | B. | B和C之间的摩擦力为30N | ||
| C. | C与桌面之间的摩擦力为10N | D. | 物块C受到5个力的作用 |
 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法正确的是( )| A. | 质点由O到达各点的时间之比ta:tb:tc:td=1:2:3:4 | |
| B. | 质点通过各点的速率之比va:vb:vc:vd=1:2:3:4 | |
| C. | 在斜面上od间运动的平均速度$\overline{v}$=vb | |
| D. | 在斜面上od间运动的平均速度$\overline{v}$=$\frac{{v}_{d}}{2}$ |

| A. | 电容器电容增大 | |
| B. | 电容器极板电荷量增加 | |
| C. | 在增大极板间距离过程中,电路中电流方向与图示方向相反 | |
| D. | 原来静止在电容器极板间的电荷将向下加速运动 |
| A. | 当物体做匀加速直线运动时V1>V2 | B. | 当物体做匀减速直线运动时V1>V2 | ||
| C. | 当物体做匀加速直线运动时V1<V2 | D. | 当物体做匀减速直线运动时V1<V2 |
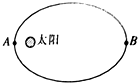 如图所示,某行星绕太阳运行的轨道是椭圆,A点是轨道上距太阳最近的位置,B点是轨道上距太阳最远的位置,行星在A点的速度( )在B点的速度.
如图所示,某行星绕太阳运行的轨道是椭圆,A点是轨道上距太阳最近的位置,B点是轨道上距太阳最远的位置,行星在A点的速度( )在B点的速度. 如图所示的电路中,R1=10Ω,R2=4Ω,R3=6Ω,R4=3Ω,U=2.4V.在ab间接一只理想电压表,它的读数是多少?如在ab间接一只理想电流表,它的读数又是多少?
如图所示的电路中,R1=10Ω,R2=4Ω,R3=6Ω,R4=3Ω,U=2.4V.在ab间接一只理想电压表,它的读数是多少?如在ab间接一只理想电流表,它的读数又是多少? 如图所示为6个质量均为m的人搭成的叠罗汉.若上面人的压力平均作用在下面的两个人肩上.求:
如图所示为6个质量均为m的人搭成的叠罗汉.若上面人的压力平均作用在下面的两个人肩上.求: