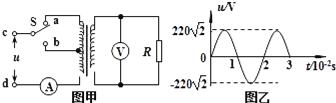
题目内容
【题目】如图所示,ABC为竖直平面内的光滑绝缘轨道,其中AB为倾斜直轨道,BC为与AB相切的圆形轨道,并且圆形轨道处在匀强磁场中,磁场方向垂直纸面向里。今有质量相同的甲、乙、丙三个小球,其中甲球带正电、乙球带负电、丙球不带电,现将三个小球在轨道AB上分别从不同高度处由静止释放,都恰好通过圆形轨道最高点,则
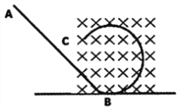
A. 经过最高点时,三个小球的速度相等
B. 经过最高点时,甲球的速度最小
C. 乙球释放的位置最高
D. 甲球下落过程中,机械能守恒
【答案】D
【解析】在最高点时,甲球受洛仑兹力向下,乙球受洛仑兹力向上,而丙球不受洛仑兹力,三球在最高点受合力不同,由牛顿第二定律得:F合=m![]() ,由F合于不同m、R相等,则三个小球经过最高点时的速度不相等,故A错误;由于经过最高点时甲球所受合力最大,甲球在最高点的速度最大,故B错误;甲球经过最高点时的速度最大,甲的机械能最大,小球在运动过程中只有重力做功,机械能守恒,由机械能守恒定律可知,甲释放时的位置最高,故C错误;洛伦兹力不做功,小球在运动过程中只有重力做功,机械能守恒,故D正确;故选D。
,由F合于不同m、R相等,则三个小球经过最高点时的速度不相等,故A错误;由于经过最高点时甲球所受合力最大,甲球在最高点的速度最大,故B错误;甲球经过最高点时的速度最大,甲的机械能最大,小球在运动过程中只有重力做功,机械能守恒,由机械能守恒定律可知,甲释放时的位置最高,故C错误;洛伦兹力不做功,小球在运动过程中只有重力做功,机械能守恒,故D正确;故选D。

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目