题目内容
如图所示,倾角37°的斜面上,轻弹簧一端固定在A点,自然状态时另一端位于B点.斜面上方有一半径R=1m、圆心角等于143°的竖直圆弧形光滑轨道与斜面相切于D处,圆弧轨道的最 高点为M.用质量为m1=6.3kg的物块将弹簧缓慢压缩至C点,由静止释放后弹簧恢复原长时物块到B点速度恰好减小为0.用同种材料、质量为m2=0.3kg的另一小物块将弹簧缓慢压缩到C点后由静止释放,物块经过B点后的位移与时间的关系为x=8t-4t2(x单位:m,t单位:s),若物块经过D点后恰能到达M点,重力加速度g=m/s2,sin37°=0.6,cos37°=0.8.
高点为M.用质量为m1=6.3kg的物块将弹簧缓慢压缩至C点,由静止释放后弹簧恢复原长时物块到B点速度恰好减小为0.用同种材料、质量为m2=0.3kg的另一小物块将弹簧缓慢压缩到C点后由静止释放,物块经过B点后的位移与时间的关系为x=8t-4t2(x单位:m,t单位:s),若物块经过D点后恰能到达M点,重力加速度g=m/s2,sin37°=0.6,cos37°=0.8.
求:
(1)物块与斜面间的动摩擦因数;
(2)BD间的距离lBD;
(3)m2从被释放至运动到M点的过程中克服摩擦力做的功W.
 高点为M.用质量为m1=6.3kg的物块将弹簧缓慢压缩至C点,由静止释放后弹簧恢复原长时物块到B点速度恰好减小为0.用同种材料、质量为m2=0.3kg的另一小物块将弹簧缓慢压缩到C点后由静止释放,物块经过B点后的位移与时间的关系为x=8t-4t2(x单位:m,t单位:s),若物块经过D点后恰能到达M点,重力加速度g=m/s2,sin37°=0.6,cos37°=0.8.
高点为M.用质量为m1=6.3kg的物块将弹簧缓慢压缩至C点,由静止释放后弹簧恢复原长时物块到B点速度恰好减小为0.用同种材料、质量为m2=0.3kg的另一小物块将弹簧缓慢压缩到C点后由静止释放,物块经过B点后的位移与时间的关系为x=8t-4t2(x单位:m,t单位:s),若物块经过D点后恰能到达M点,重力加速度g=m/s2,sin37°=0.6,cos37°=0.8.求:
(1)物块与斜面间的动摩擦因数;
(2)BD间的距离lBD;
(3)m2从被释放至运动到M点的过程中克服摩擦力做的功W.
分析:(1)由x=8t-4t2分析出物块经过B速度,B到D过程的加速度,根据牛顿第二定律求解物块与斜面间的动摩擦因数;
(2)物块经过D点后恰能到达M点时,由重力提供向心力,由牛顿第二定律求出物块经过M点的速度,物块D到M的过程中,只有重力做功,机械能守恒,可求出物块经过D点的速度,由运动学公式求出BD间的距离lBD;
(3)两个物体从C到B过程,弹簧弹力做功相同,分别对两个物体研究C到B过程,可求出lCB,即可求出m2从被释放至运动到M点的过程中克服摩擦力做的功W.
(2)物块经过D点后恰能到达M点时,由重力提供向心力,由牛顿第二定律求出物块经过M点的速度,物块D到M的过程中,只有重力做功,机械能守恒,可求出物块经过D点的速度,由运动学公式求出BD间的距离lBD;
(3)两个物体从C到B过程,弹簧弹力做功相同,分别对两个物体研究C到B过程,可求出lCB,即可求出m2从被释放至运动到M点的过程中克服摩擦力做的功W.
解答:解:(1)由物块经物块经过B点后的位移与时间的关系为x=8t-4t2,可知,物块经过B点时的速度为vB=8m/s,从B到D的过程中加速度大小为a=8m/s2.
根据牛顿第二定律,有
mgsin37°+μmgcos37°=ma
解得,μ=0.25
(2)设物块经过M点的速度为vM,由牛顿第二定律得
mg=
物块从D到M的过程中,根据机械能守恒定律得
m
=mgR(1+cos37°)+
m
物块从B到D的过程中,有
-
=-2alBD
解得,lBD=
m
(2)设物块由C到B过程弹簧弹力做的功为W弹,对m1、m2,由C到B的过程,
根据动能定理,分别有
-μm1glCBcos37°-m1glCBsin37°+W弹=0
-μm2glCBcos37°-m2glCBsin37°+W弹=
m2
又W=μm2gcos37°(lCB+lBD)
解得,W=0.795J
答:
(1)物块与斜面间的动摩擦因数是0.25;
(2)BD间的距离lBD是
m.
(3)m2从被释放至运动到M点的过程中克服摩擦力做的功W是0.795J.
根据牛顿第二定律,有
mgsin37°+μmgcos37°=ma
解得,μ=0.25
(2)设物块经过M点的速度为vM,由牛顿第二定律得
mg=
m
| ||
| R |
物块从D到M的过程中,根据机械能守恒定律得
| 1 |
| 2 |
| v | 2 D |
| 1 |
| 2 |
| v | 2 M |
物块从B到D的过程中,有
| v | 2 D |
| v | 2 B |
解得,lBD=
| 9 |
| 8 |
(2)设物块由C到B过程弹簧弹力做的功为W弹,对m1、m2,由C到B的过程,
根据动能定理,分别有
-μm1glCBcos37°-m1glCBsin37°+W弹=0
-μm2glCBcos37°-m2glCBsin37°+W弹=
| 1 |
| 2 |
| v | 2 B |
又W=μm2gcos37°(lCB+lBD)
解得,W=0.795J
答:
(1)物块与斜面间的动摩擦因数是0.25;
(2)BD间的距离lBD是
| 9 |
| 8 |
(3)m2从被释放至运动到M点的过程中克服摩擦力做的功W是0.795J.
点评:本题是力学综合题,分析过程是基础,把握解题规律是关键,要抓住C到B过程中,弹簧的弹力做功相同.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 如图所示,倾角θ=37°的斜面足够长,质量m=1kg的滑块静置在斜面的底端A点,滑块与斜面间的动摩擦因素为μ=0.5.现给滑块一个沿斜面向上v°=10m/s的初速度,同时用水平恒力F向右推,使滑块做匀加速运动,在2s后撤去推力F,滑块再运动3s时经过B点,已知AB间距x0=49m,(已知sin37°=0.6,cos37°=0.8).求:
如图所示,倾角θ=37°的斜面足够长,质量m=1kg的滑块静置在斜面的底端A点,滑块与斜面间的动摩擦因素为μ=0.5.现给滑块一个沿斜面向上v°=10m/s的初速度,同时用水平恒力F向右推,使滑块做匀加速运动,在2s后撤去推力F,滑块再运动3s时经过B点,已知AB间距x0=49m,(已知sin37°=0.6,cos37°=0.8).求: 如图所示,倾角θ=37°的传送带上,上、下两端相距S=7m.当传送带以μ=4m/s的恒定速率逆时针转动时,将一个与传送带间动摩擦因数μ=0.25的物块P轻放于A端,P从A端运动到B端所需的时间是多少?若传送带顺时针转动,P从A端运动到B端的时间又是多少?
如图所示,倾角θ=37°的传送带上,上、下两端相距S=7m.当传送带以μ=4m/s的恒定速率逆时针转动时,将一个与传送带间动摩擦因数μ=0.25的物块P轻放于A端,P从A端运动到B端所需的时间是多少?若传送带顺时针转动,P从A端运动到B端的时间又是多少?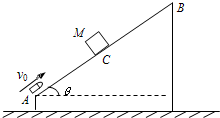 如图所示,倾角θ=37°的固定斜面AB长L=18.4m,质量为M=1kg的木块由斜面中点C从静止开始下滑,0.5s后被一颗质量为m=20g的子弹以v0=500m/s沿斜面向上的速度正对射入并穿出,穿出速度u=200m/s.以后每隔1.0s就有一颗子弹射入木块,设子弹射穿木块的时间极短,且每次射入木块对子弹的阻力相同.已知木块与斜面间的动摩擦因数μ=0.25,g取10m/s2,sin37°=0.60,cos37°=0.80,求:
如图所示,倾角θ=37°的固定斜面AB长L=18.4m,质量为M=1kg的木块由斜面中点C从静止开始下滑,0.5s后被一颗质量为m=20g的子弹以v0=500m/s沿斜面向上的速度正对射入并穿出,穿出速度u=200m/s.以后每隔1.0s就有一颗子弹射入木块,设子弹射穿木块的时间极短,且每次射入木块对子弹的阻力相同.已知木块与斜面间的动摩擦因数μ=0.25,g取10m/s2,sin37°=0.60,cos37°=0.80,求: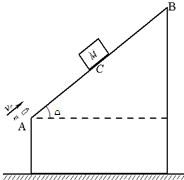 如图所示,倾角θ=37°的固定斜面AB长L=18m,质量为M=1kg的木块由斜面中点C从静止开始下滑,0.5s后被一颗质量为m=20g的子弹以v0=600m/s沿斜面向上的速度正对射入并穿出,穿出速度u=100m/s.以后每隔1.5s就有一颗子弹射入木块,设子弹射穿木块的时间极短,且每次射入木块对子弹的阻力相同.已知木块与斜面间的动摩擦因数μ=0.25,g取10m/s2,sin37°=0.60,cos37=0.80°.求:
如图所示,倾角θ=37°的固定斜面AB长L=18m,质量为M=1kg的木块由斜面中点C从静止开始下滑,0.5s后被一颗质量为m=20g的子弹以v0=600m/s沿斜面向上的速度正对射入并穿出,穿出速度u=100m/s.以后每隔1.5s就有一颗子弹射入木块,设子弹射穿木块的时间极短,且每次射入木块对子弹的阻力相同.已知木块与斜面间的动摩擦因数μ=0.25,g取10m/s2,sin37°=0.60,cos37=0.80°.求: