题目内容
一水平传送带以2.0m/s的速度匀速运动，某工件与传送带间的动摩擦因数为0.2，现将该工件轻放到传送
带上，此时工件的加速度为
带上，此时工件的加速度为
2
2
m/s2，经过时间1
1
s工件的速度达到2.0m/s．（g取10m/s2）分析：工件轻放到传送带上，初速度为零，做初速度为零的匀加速运动；受重力、支持力和向前的滑动摩擦力，根据牛顿第二定律列式求解加速度；然后根据v=at求解加速时间．
解答：解：工件轻放到传送带上，初速度为零，做初速度为零的匀加速运动；
受重力、支持力和向前的滑动摩擦力，根据牛顿第二定律，有：
N=mg
f=ma
其中：f=μN
联立解得：a=μg=0.2×10=2m/s2
根据速度时间关系公式，有：
v=at
解得：t=
=
=1s
故答案为：2，1．
受重力、支持力和向前的滑动摩擦力，根据牛顿第二定律，有：
N=mg
f=ma
其中：f=μN
联立解得：a=μg=0.2×10=2m/s2
根据速度时间关系公式，有：
v=at
解得：t=
| v |
| a |
| 2 |
| 2 |
故答案为：2，1．
点评：本题是已知受力情况确定运动情况，关键先根据牛顿第二定律求解加速度，然后根据运动学公式求解时间．
练习册系列答案
相关题目
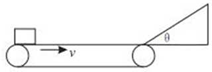如图所示，一水平传送带以2.0m/s的速度顺时针传动．水平部分长为2.0m．其右端与一倾角为θ=370的光滑斜面平滑相连．斜面长为0.4m，-个可视为质 点的物块无初速度地放在传送带最左端．已知物块与传送带间动莩擦因数μ=0.2，sin37°=0.6，g取 10m/s2．则（ ）
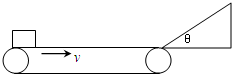一水平传送带以2.0m/s的速度顺时针传动，水平部分长为2.0m．，其右端与一倾角为θ=37°的光滑斜面平滑相连，斜面长为0.4m，一个可视为质点的物块无初速度地放在传送带最左端，已知物块与传送带间动摩擦因数μ=0.2，试问：
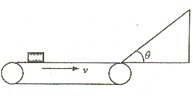一水平传送带以2.0m/s的速度顺时针传动，水平部分长为2.0m．，其右端与一倾角为θ=37°的光滑斜面平滑相连，斜面长为0.4m，一个可视为质点的物块无初速度地放在传送带最左端，已知物块与传送带间动摩擦因数μ=0.2，则（ ）