题目内容
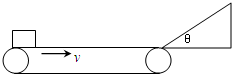 一水平传送带以2.0m/s的速度顺时针传送,水平部分长为2.0m,其右端与一倾角为θ=37°的光滑斜面平滑相连,斜面长为0.4m,一个可视为质点物块无初速度地放在传送带最左端,已知物块与传送带间动摩擦因数μ=0.2,试问:
一水平传送带以2.0m/s的速度顺时针传送,水平部分长为2.0m,其右端与一倾角为θ=37°的光滑斜面平滑相连,斜面长为0.4m,一个可视为质点物块无初速度地放在传送带最左端,已知物块与传送带间动摩擦因数μ=0.2,试问:(1)物块能否达斜面顶端?若能则说明理由,若不能则求出物块上升的最大高度.
(2)出发后9.5s内物块运动的路程.(sin37°=0.6,g取10m/s2)
分析:(1)对物块进行受力分析,找出物块的合力,明确其运动性质,运用牛顿第二定律和运动学公式去求解到达传送带右端时的速度.物块冲上斜面后做匀减速直线运动,先根据运动学公式求出上物块运动的最大位移(到达最大位移时速度为0),然后与题目中的斜面长对比即可求解.
(2)根据运动学方程可求出物体运动的周期,从而可确定物体在9.5s内的完成多少次,进而可算出运动的路程.
(2)根据运动学方程可求出物体运动的周期,从而可确定物体在9.5s内的完成多少次,进而可算出运动的路程.
解答:解:(1)物块在传送带上先加速后匀速,在摩擦力作用下产生加速度大小为:a1=μg=2(m/s2)
物体做匀加速运动的时间为:t1=
=1(s);
匀加速运动的距离为:S1=
a1
=1(m)
剩下物体匀速距离为:S2=L-S1=1(m);匀速时间为:t2=
=0.5(s)
然后物块以2m/s的速度滑上斜面,
因为斜面光滑,所以物体在斜面上运动的加速度大小为:a2=gsinθ=6(m/s2)
上升过程历时:t3=
=
(s);上升距离S3=
=
(m)<0.4m.
所以没有到最高点,上升高度为h=S3sinθ=0.2(m)
(2)物块的运动全过程为:
先匀加速1s,匀速运动0.5s,在斜面上匀减速上升
s,在斜面上匀加速下降
s后回到传送带,再经过1s速度减为零,然后加速1s运动到斜面底端…如此往复,周期为
s.
由第一次到达斜面底端算起,还剩8s,恰好完成三个周期∴S=L+6(S1+S3)=10(m)
答:(1)不能到达斜面顶端,上升的最大高度为0.2m;
(2)出发后9.5s内物体的路程为10m.
物体做匀加速运动的时间为:t1=
| v0 |
| a1 |
匀加速运动的距离为:S1=
| 1 |
| 2 |
| t | 2 1 |
剩下物体匀速距离为:S2=L-S1=1(m);匀速时间为:t2=
| S2 |
| v0 |
然后物块以2m/s的速度滑上斜面,
因为斜面光滑,所以物体在斜面上运动的加速度大小为:a2=gsinθ=6(m/s2)
上升过程历时:t3=
| v0 |
| a2 |
| 1 |
| 3 |
| ||
| 2a2 |
| 1 |
| 3 |
所以没有到最高点,上升高度为h=S3sinθ=0.2(m)
(2)物块的运动全过程为:
先匀加速1s,匀速运动0.5s,在斜面上匀减速上升
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
由第一次到达斜面底端算起,还剩8s,恰好完成三个周期∴S=L+6(S1+S3)=10(m)
答:(1)不能到达斜面顶端,上升的最大高度为0.2m;
(2)出发后9.5s内物体的路程为10m.
点评:本题要注意物体刚放在传送带上时在滑动摩擦力作用下做匀加速运动,速度达到传送带速度后与传送带一起做匀速运动,此时不受摩擦力作用,能否到达最高点我们也可以根据动能定理去求解,难度适中.同时通过物体的多过程运动分析,从而确定在规定时间内的运动次数并能确定总路程.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
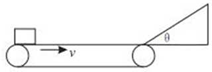 如图所示,一水平传送带以2.0m/s的速度顺时针传动.水平部分长为2.0m.其右端与一倾角为θ=370的光滑斜面平滑相连.斜面长为0.4m,-个可视为质 点的物块无初速度地放在传送带最左端.已知物块与传送带间动莩擦因数μ=0.2,sin37°=0.6,g取 10m/s2.则( )
如图所示,一水平传送带以2.0m/s的速度顺时针传动.水平部分长为2.0m.其右端与一倾角为θ=370的光滑斜面平滑相连.斜面长为0.4m,-个可视为质 点的物块无初速度地放在传送带最左端.已知物块与传送带间动莩擦因数μ=0.2,sin37°=0.6,g取 10m/s2.则( )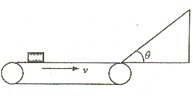 一水平传送带以2.0m/s的速度顺时针传动,水平部分长为2.0m.,其右端与一倾角为θ=37°的光滑斜面平滑相连,斜面长为0.4m,一个可视为质点的物块无初速度地放在传送带最左端,已知物块与传送带间动摩擦因数μ=0.2,则( )
一水平传送带以2.0m/s的速度顺时针传动,水平部分长为2.0m.,其右端与一倾角为θ=37°的光滑斜面平滑相连,斜面长为0.4m,一个可视为质点的物块无初速度地放在传送带最左端,已知物块与传送带间动摩擦因数μ=0.2,则( )