题目内容
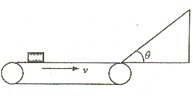 一水平传送带以2.0m/s的速度顺时针传动,水平部分长为2.0m.,其右端与一倾角为θ=37°的光滑斜面平滑相连,斜面长为0.4m,一个可视为质点的物块无初速度地放在传送带最左端,已知物块与传送带间动摩擦因数μ=0.2,则( )
一水平传送带以2.0m/s的速度顺时针传动,水平部分长为2.0m.,其右端与一倾角为θ=37°的光滑斜面平滑相连,斜面长为0.4m,一个可视为质点的物块无初速度地放在传送带最左端,已知物块与传送带间动摩擦因数μ=0.2,则( )分析:对物块进行受力分析,找出物块的合力,明确其运动性质,运用牛顿第二定律和运动学公式去求解到达传送带右端时的速度.物块冲上斜面后做匀减速直线运动,先根据运动学公式求出上物块运动的最大位移(到达最大位移时速度为0),然后与题目中的斜面长对比即可求解.
解答:解:物块在传送带上先做匀加速直线运动:
μmg=mal
al=2m/s2
当两者速度相等时,t=
=
=1s
此时物块运动的位移为:s1=
a1t2=
×2×1m=1m<2m
所以在到达传送带右端前物块已匀速,速度为2m/s
物块以ν0速度滑上斜面
-mgsinθ=ma2
a2=-6m/s2
物块速度为零时上升的距离
s2=
=
=
m
由于s2<0.4m,所以物块未到达斜面的最高点.
物块上升的最大高度:
hm=s2sinθ=0.2m,故A错误,B正确;
物块返回皮带时滑的距离为x,则mghm-μmgx=0,x=1m,所以物块返回皮带时不会到达最左端,故D错误.
根据能量守恒可知,物块每次返回的距离逐渐变小,最终会停在最右端,故C正确.
故选BC
μmg=mal
al=2m/s2
当两者速度相等时,t=
| v |
| a1 |
| 2 |
| 2 |
此时物块运动的位移为:s1=
| 1 |
| 2 |
| 1 |
| 2 |
所以在到达传送带右端前物块已匀速,速度为2m/s
物块以ν0速度滑上斜面
-mgsinθ=ma2
a2=-6m/s2
物块速度为零时上升的距离
s2=
| 0-v2 |
| 2a2 |
| 0-4 |
| -12 |
| 1 |
| 3 |
由于s2<0.4m,所以物块未到达斜面的最高点.
物块上升的最大高度:
hm=s2sinθ=0.2m,故A错误,B正确;
物块返回皮带时滑的距离为x,则mghm-μmgx=0,x=1m,所以物块返回皮带时不会到达最左端,故D错误.
根据能量守恒可知,物块每次返回的距离逐渐变小,最终会停在最右端,故C正确.
故选BC
点评:本题要注意物体刚放在传送带上时在滑动摩擦力作用下做匀加速运动,速度达到传送带速度后与传送带一起做匀速运动,此时不受摩擦力作用,能否到达最高点我们也可以根据动能定理去求解,难度适中.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
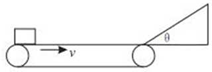 如图所示,一水平传送带以2.0m/s的速度顺时针传动.水平部分长为2.0m.其右端与一倾角为θ=370的光滑斜面平滑相连.斜面长为0.4m,-个可视为质 点的物块无初速度地放在传送带最左端.已知物块与传送带间动莩擦因数μ=0.2,sin37°=0.6,g取 10m/s2.则( )
如图所示,一水平传送带以2.0m/s的速度顺时针传动.水平部分长为2.0m.其右端与一倾角为θ=370的光滑斜面平滑相连.斜面长为0.4m,-个可视为质 点的物块无初速度地放在传送带最左端.已知物块与传送带间动莩擦因数μ=0.2,sin37°=0.6,g取 10m/s2.则( )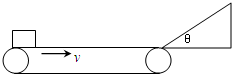 一水平传送带以2.0m/s的速度顺时针传动,水平部分长为2.0m.,其右端与一倾角为θ=37°的光滑斜面平滑相连,斜面长为0.4m,一个可视为质点的物块无初速度地放在传送带最左端,已知物块与传送带间动摩擦因数μ=0.2,试问:
一水平传送带以2.0m/s的速度顺时针传动,水平部分长为2.0m.,其右端与一倾角为θ=37°的光滑斜面平滑相连,斜面长为0.4m,一个可视为质点的物块无初速度地放在传送带最左端,已知物块与传送带间动摩擦因数μ=0.2,试问: