题目内容
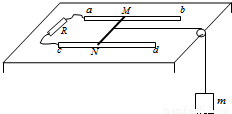 如图所示,相距为l的光滑平行金属导轨ab、cd放置在水平桌面上,阻值为R的电阻与导轨的两端a、c相连.滑杆MN质量为m,垂直于导轨并可在导轨上自由滑动,不计导轨、滑杆以及导线的电阻.整个装置放于竖直方向的范围足够大的匀强磁场中,磁感应强度的大小为B.滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与另一质量也为m的物块相连,绳处于拉直状态.现将物块由静止释放,当物块达到最大速度时,物块的下落高度
如图所示,相距为l的光滑平行金属导轨ab、cd放置在水平桌面上,阻值为R的电阻与导轨的两端a、c相连.滑杆MN质量为m,垂直于导轨并可在导轨上自由滑动,不计导轨、滑杆以及导线的电阻.整个装置放于竖直方向的范围足够大的匀强磁场中,磁感应强度的大小为B.滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与另一质量也为m的物块相连,绳处于拉直状态.现将物块由静止释放,当物块达到最大速度时,物块的下落高度 ,用g表示重力加速度,则在物块由静止开始下落至速度最大的过程中( )
,用g表示重力加速度,则在物块由静止开始下落至速度最大的过程中( )A.物块达到的最大速度是

B.通过电阻R的电荷量是
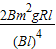
C.电阻R放出的热量为

D.滑杆MN产生的最大感应电动势为

【答案】分析:当棒子所受的安培力等于绳子拉力时,速度最大,根据平衡,结合闭合电路欧姆定律求出最大速度.根据能量守恒求出此过程中电阻R上放出的热量.求出速度最大时的感应电动势大小,从而根据功率的公式求出电阻R上消耗的功率.
解答:解:A、当FA=mg时,速度最大,有: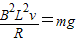 ,则最大速度v=
,则最大速度v=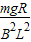 .故A正确,
.故A正确,
B、通过电阻R的横截面积的电荷量q=It=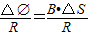 =
=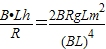 ,故B正确;
,故B正确;
C、根据能量守恒得,mgh= mv2+Q,解得Q=mgh-
mv2+Q,解得Q=mgh- mv2=
mv2=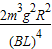
 =
=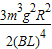 .故C错误.
.故C错误.
D、物块速度最大时,产生的感应电动势E=Blv=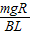 .故D正确.
.故D正确.
故选ABD.
点评:解决本题的关键知道当棒子所受的安培力和绳子拉力相等时,速度最大.以及会根据能量守恒定律求出电阻R上消耗的热量.
解答:解:A、当FA=mg时,速度最大,有:
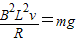 ,则最大速度v=
,则最大速度v=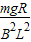 .故A正确,
.故A正确,B、通过电阻R的横截面积的电荷量q=It=
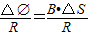 =
=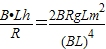 ,故B正确;
,故B正确;C、根据能量守恒得,mgh=
 mv2+Q,解得Q=mgh-
mv2+Q,解得Q=mgh- mv2=
mv2=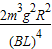
 =
=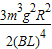 .故C错误.
.故C错误.D、物块速度最大时,产生的感应电动势E=Blv=
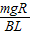 .故D正确.
.故D正确.故选ABD.
点评:解决本题的关键知道当棒子所受的安培力和绳子拉力相等时,速度最大.以及会根据能量守恒定律求出电阻R上消耗的热量.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
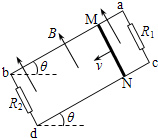 如图所示,相距为L的平行金属导轨ab、cd与水平面成θ角放置,导轨与阻值均为R的两定值电阻R1、R2相连,磁感应强度为B的匀强磁场垂直穿过导轨平面.有一质量为m、阻值也为R的导体棒MN,以速度v沿导轨匀速下滑,它与导轨之间的动摩擦因数为μ,忽略感应电流之间的相互作用,则( )
如图所示,相距为L的平行金属导轨ab、cd与水平面成θ角放置,导轨与阻值均为R的两定值电阻R1、R2相连,磁感应强度为B的匀强磁场垂直穿过导轨平面.有一质量为m、阻值也为R的导体棒MN,以速度v沿导轨匀速下滑,它与导轨之间的动摩擦因数为μ,忽略感应电流之间的相互作用,则( )A、导体棒下滑的速度大小为
| ||
B、电阻R1消耗的热功率为
| ||
C、导体棒两端电压为
| ||
D、t时间内通过导体棒的电荷量为
|
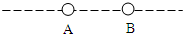 如图所示,相距为L的点电荷A、B的带电量分为+4Q和-Q,要引进第三个点电荷C,使三个点电荷在库仑力作用下都能处于平衡状态,试求C电荷的电量和放置的位置?
如图所示,相距为L的点电荷A、B的带电量分为+4Q和-Q,要引进第三个点电荷C,使三个点电荷在库仑力作用下都能处于平衡状态,试求C电荷的电量和放置的位置?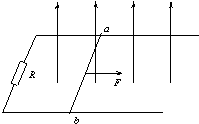 .如图所示,相距为L的足够长的光滑平行金属导轨水平放置,处于磁感应强度为B,方向竖直向上的匀强磁场中.导轨一端连接一阻值为R的电阻,导轨本身的电阻不计,一质量为m,电阻为r的金属棒ab横跨在导轨上.现对金属棒施一外力F,使其从静止开始运动,运动过程中外力F的功率恒定为P0.求:
.如图所示,相距为L的足够长的光滑平行金属导轨水平放置,处于磁感应强度为B,方向竖直向上的匀强磁场中.导轨一端连接一阻值为R的电阻,导轨本身的电阻不计,一质量为m,电阻为r的金属棒ab横跨在导轨上.现对金属棒施一外力F,使其从静止开始运动,运动过程中外力F的功率恒定为P0.求: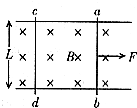 (2005?和平区一模)如图所示,相距为L的两条足够长的光滑平行轨道上,平行放置两根质量和电阻都相同的滑杆ab和cd,组成矩形闭合回路.轨道电阻不计,匀强磁场B垂直穿过整个轨道平面.开始时ab与cd均处于静止状态,现用一个平行轨道的恒力F向右拉ab杆,则下列说法中正确的是( )
(2005?和平区一模)如图所示,相距为L的两条足够长的光滑平行轨道上,平行放置两根质量和电阻都相同的滑杆ab和cd,组成矩形闭合回路.轨道电阻不计,匀强磁场B垂直穿过整个轨道平面.开始时ab与cd均处于静止状态,现用一个平行轨道的恒力F向右拉ab杆,则下列说法中正确的是( )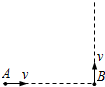 如图所示,相距为L的A、B两质点沿相互垂直的两个方向以相同的速率v做匀速直线运动,则在运动过程中,A、B间的最短距离为( )
如图所示,相距为L的A、B两质点沿相互垂直的两个方向以相同的速率v做匀速直线运动,则在运动过程中,A、B间的最短距离为( )