题目内容
 如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角.若在B点悬挂一个定滑轮(不计重力),某人用它提起重物,使重物以加速度2m/s2向上做匀加速运动.已知重物的质量 m=10kg,人的质量M=50kg,g取10m/s2.试求:
如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角.若在B点悬挂一个定滑轮(不计重力),某人用它提起重物,使重物以加速度2m/s2向上做匀加速运动.已知重物的质量 m=10kg,人的质量M=50kg,g取10m/s2.试求:
(1)此时绳对重物的拉力和地面对人的支持力的大小;
(2)轻杆BC和绳AB所受力的大小.
解:(1)物体m向上加速,设绳中拉力为T.
对m有:T-mg=ma T=m(g+a)=10×12N
解得:T=120N.
人静止在地面上,受力平衡.地面对人的支持力:N=Mg-T=500-120=380N.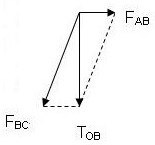
(2)由图知 绳OB中拉力TOB=2T=240N.
对B点:受三个力作用而平衡
FBCcos30°=TOB
FBCsin30°=FAB
解得:FBC=160 N,FAB=80
N,FAB=80 N.
N.
答:(1)绳对重物的拉力和地面对人的支持力的大小分别为120N,380N.
(2)轻杆BC和绳AB所受力的大小分别为160 N,80
N,80 N.
N.
分析:要使重物以加速度2m/s2向上做匀加速运动,由牛顿第二定律F=ma可求,绳对重物的拉力,地面对人的支持力的大小可由人的受力平衡来求,根据共点力平衡的条件,轻杆BC和绳AB所受力的大小可由力的矢量三角形中求得.
点评:共点力平衡问题中,选准研究对象很关键,然后根据力的效果画出力的矢量三角形,由已知的力求出未知的力.
对m有:T-mg=ma T=m(g+a)=10×12N
解得:T=120N.
人静止在地面上,受力平衡.地面对人的支持力:N=Mg-T=500-120=380N.

(2)由图知 绳OB中拉力TOB=2T=240N.
对B点:受三个力作用而平衡
FBCcos30°=TOB
FBCsin30°=FAB
解得:FBC=160
 N,FAB=80
N,FAB=80 N.
N.答:(1)绳对重物的拉力和地面对人的支持力的大小分别为120N,380N.
(2)轻杆BC和绳AB所受力的大小分别为160
 N,80
N,80 N.
N.分析:要使重物以加速度2m/s2向上做匀加速运动,由牛顿第二定律F=ma可求,绳对重物的拉力,地面对人的支持力的大小可由人的受力平衡来求,根据共点力平衡的条件,轻杆BC和绳AB所受力的大小可由力的矢量三角形中求得.
点评:共点力平衡问题中,选准研究对象很关键,然后根据力的效果画出力的矢量三角形,由已知的力求出未知的力.

练习册系列答案
相关题目
 如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角.若在B点悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg,g取10m/s2.试求:
如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角.若在B点悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg,g取10m/s2.试求: 如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB连接使杆与竖直墙壁保持30°的夹角.若在B点通过BO绳悬挂一个定滑轮(不计滑轮重力及摩擦),某人用跨在滑轮上的细绳匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg,g取10m/s2.试求:
如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB连接使杆与竖直墙壁保持30°的夹角.若在B点通过BO绳悬挂一个定滑轮(不计滑轮重力及摩擦),某人用跨在滑轮上的细绳匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg,g取10m/s2.试求: 如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过细绳AB使杆水平、细线与竖直墙壁保持30°的夹角.若在B点悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg.试求:
如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过细绳AB使杆水平、细线与竖直墙壁保持30°的夹角.若在B点悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg.试求: 如图所示,轻杆BC的一端铰接于C,另一端悬挂重物G,并用细绳绕过定滑轮用力拉住.开始时,∠BCA>90°,现用拉力F使∠BCA缓慢减小,直到BC接近竖直位置的过程中,杆BC所受的压力( )
如图所示,轻杆BC的一端铰接于C,另一端悬挂重物G,并用细绳绕过定滑轮用力拉住.开始时,∠BCA>90°,现用拉力F使∠BCA缓慢减小,直到BC接近竖直位置的过程中,杆BC所受的压力( ) 如图所示,轻杆BC的一端铰接于C,另一端挂重物G,并用细绳绕过定滑轮拉住.开始时BC向下倾斜,现用力F拉绳,使BC缓慢接近竖直位置,在此过程中BC受到的圧力( )
如图所示,轻杆BC的一端铰接于C,另一端挂重物G,并用细绳绕过定滑轮拉住.开始时BC向下倾斜,现用力F拉绳,使BC缓慢接近竖直位置,在此过程中BC受到的圧力( )