题目内容
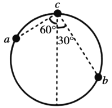
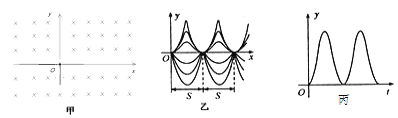
【题目】12. 如甲图所示,xOy平面位于竖直面内,匀强磁场垂直于xOy平面向里,磁感应强度大小为B。一质量为m,带电量为q(q>0)的微粒从坐标原点O处垂直磁场射入,微粒的运动轨迹由初速度的大小和方向决定。
(1)若微粒的运动轨迹为直线,那么微粒的初速度大小是多少,方向又如何?
(2)若微粒的重力很小可忽略,微粒做周期性运动,其运动周期是多少?
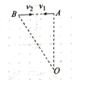
(3)若微粒的重力不可忽略,且射入速度不同于第(1)题,那么其运动轨迹为如图乙所示的周期性曲线(画出不同初速度条件下的多条运动轨迹)。从运动的合成与分解角度而言,一个复杂的曲线运动可以分解为正交两个方向的直线运动,即化曲为直的方法;也可以分解为一个直线运动和一个圆周运动,即化曲为直与化曲为圆结合方法。试着运用运动的合成与分解求解下列问题。
a.粒子在一个时间周期内,沿x轴方向前进的空间周期S;
b.以初速度v0沿x轴方向射入时,其y-t图象如图乙所示,写出y-t的函数表达式。
【答案】(1)![]() ,沿x轴正方向;(2)
,沿x轴正方向;(2)![]() ;(3)(a)
;(3)(a)![]() ,(b)
,(b)![]() 。
。
【解析】
(1)微粒的运动轨迹是直线时,微粒做匀速直线运动,洛伦兹力与重力是一对平衡力,即有
![]()
所以,初速度大小为
![]()
方向沿x轴正方向。
(2)微粒的重力很小可忽略时,微粒做匀速圆周运动,即有
![]()
![]()
于是解得:时间周期
![]() 。
。
(3)在坐标原点O处对带电粒子进行受力分析,受到沿y轴负方向的重力
![]()
和y轴正方向的洛伦兹力
![]()
当![]() 时,带电粒子做周期性曲线运动。为了把曲线运动分解为匀速圆周运动和匀速直线运动两种最简单的运动形式,构造一对平衡洛伦兹力,它们分别沿y轴正、负方向,大小等于
时,带电粒子做周期性曲线运动。为了把曲线运动分解为匀速圆周运动和匀速直线运动两种最简单的运动形式,构造一对平衡洛伦兹力,它们分别沿y轴正、负方向,大小等于
![]()
其中![]() 。重新组合,沿y轴正方向的
。重新组合,沿y轴正方向的![]() 与G重新构成一对平衡力,沿y轴负方向的
与G重新构成一对平衡力,沿y轴负方向的![]() 与f0构成合洛伦兹力
与f0构成合洛伦兹力
![]()
其中
![]()
那么,曲线运动分解为以速度v1向右的匀速直线运动和由洛伦兹力![]() 提供向心力的匀速圆周运动。这两个分运动之间相互独立,互不影响,但是具有同时性。
提供向心力的匀速圆周运动。这两个分运动之间相互独立,互不影响,但是具有同时性。
(a)综上处理与分析,由运动合成与分解原理可知,周期性曲线运动的时间周期T由匀速圆周运动这一分运动决定, x轴方向上的空间周期与匀速直线运动有关,即空间周期
![]()
(b)坐标y随时间的关系由匀速圆周分运动决定,其角速度
![]()
t时刻转过的角度为
![]()
圆周运动半径
![]()
由几何关系知
![]()
即:
![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案