题目内容
【题目】如图所示，在倾角θ=30°的光滑斜面上，物块A、B质量分别为m和2m，物块A静止在轻弹簧上面，物块B用细线与斜面顶端相连，A、B紧挨在一起但A，B之间无弹力，已知重力加速度为g．某时刻将细线剪断，则在细线剪断瞬间，下列说法正确的是（ ）
A.物块B的加速度为 
B.物块A，B间的弹力为 
C.弹簧的弹力为 
D.物块A的加速度为 
【答案】D
【解析】解：C、剪断细绳前，弹簧的弹力：F弹=mgsin30°= 
mg，细线剪断的瞬间，弹簧的弹力不变，F弹= mg，C不符合题意；
A、剪断细线瞬间，对A、B系统，加速度：a= 
= 
g，A不符合题意，D符合题意；
B、对B，由牛顿第二定律得：2mgsin30°﹣N=2ma，解得：N= mg，B不符合题意．
故答案为：D．
细线剪断的瞬间，弹簧的弹力不变，剪断细线瞬间，对A、B整体受力分析可求加速度，、对B，由牛顿第二定律列式可求弹力。
练习册系列答案
相关题目
【题目】某同学要探究弹力和弹簧伸长的关系，并测弹簧的劲度系数k．做法是先将待测弹簧的一端固定在铁架台上．然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧，并使弹簧另一端的指针恰好落在刻度尺上，当弹簧自然下垂时，指针指示的刻度值记作l0 ， 弹簧下端每增加一个50g的砝码时，指针示数分别记作l1、l2、…l5 ， g取9.8m/s2 ．
（1）下表记录的是该同学测出的5个值，其中l0未记录．
代表符号 | l0 | l1 | l2 | l3 | l4 | l5 |
刻度值/cm | 3.40 | 5.10 | 6.85 | 8.60 | 10.30 |
以砝码的数目n为纵轴，以弹簧的长度l为横轴，根据表格中的数据，在如下坐标纸中作出n﹣l图线．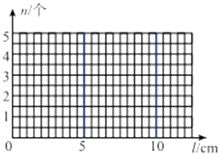
（2）根据n﹣l图线，可知弹簧的劲度系数k=N/m．（保留2位有效数字）
（3）根据n﹣l图线，可知弹簧的原长l0=cm．
