题目内容
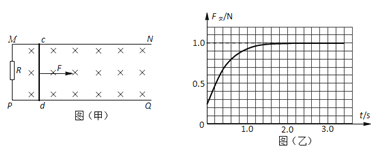
【题目】如图所示,水平圆形转台能绕过圆心的竖直转轴转动,转台半径R=1m,在转台的边缘叠放物体A、B(均可看作质点),A,B之间的动摩擦因数μ1=0.6,B与转台之间动摩擦因数μ2=0.8,且mA=2kg,mB=4kg,(g取10m/s2,设最大静摩擦力等于滑动摩擦力)求:

(1)若开始的时候转台边缘只放上了B物体,如图a,求随着转速的增加,B物体即将发生滑动时所对应的角速度ω0;
(2)当物体A、B叠放在一起的时候,转台以ω1=2rad/s匀速转动,如图b,求此时转台对B的摩擦力大小;
(3)现用一根长l=![]() m的轻绳将B,C相连,轻绳能够承受的最大拉力为
m的轻绳将B,C相连,轻绳能够承受的最大拉力为![]() N,C物体(可看作质点)的质量mC=1kg,在让转台从静止缓慢加速转动至ω2=
N,C物体(可看作质点)的质量mC=1kg,在让转台从静止缓慢加速转动至ω2=![]() rad/s的过程中,如图c,求转台对B的摩擦力第一次发生突变时的角速度,并写出突变后转台对B的摩擦力与角速度的函数关系.
rad/s的过程中,如图c,求转台对B的摩擦力第一次发生突变时的角速度,并写出突变后转台对B的摩擦力与角速度的函数关系.
【答案】(1)![]() (2)
(2)![]() (3)
(3) ![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]()
【解析】(1)由![]()
解出: ![]()
(2)A、B相对滑动时: ![]()
解出: ![]() ,
, ![]() 说明一起转动
说明一起转动
则: ![]()
解出:f=24N
(3)转台对B的摩擦力第一次发生突变时:Tcosθ=mcg
![]()
解出: ![]()
分析可得第一次发生突变后:
当![]() 时,
时, ![]()
当![]() 时,
时, ![]()

练习册系列答案
相关题目