题目内容
9. 我国的航空航天事业取得了巨大成就.2013年12月14日,“嫦娥三号”探测器在月球上的虹湾区成功实现软着陆.“嫦娥三号”在着陆前经历了发射入轨、地月转移、环月飞行等一系列过程,右图为“嫦娥三号”的飞行轨道示意图.当“嫦娥三号”在环月段上做匀速圆周运动时,运行轨道距离月球表面的高度为H,已知月球的质量为M,“嫦娥三号”的质量为m,月球半径为R月,引力常量G.忽略月球自转影响.求“嫦娥三号”在环月段上做匀速圆周运动时:
我国的航空航天事业取得了巨大成就.2013年12月14日,“嫦娥三号”探测器在月球上的虹湾区成功实现软着陆.“嫦娥三号”在着陆前经历了发射入轨、地月转移、环月飞行等一系列过程,右图为“嫦娥三号”的飞行轨道示意图.当“嫦娥三号”在环月段上做匀速圆周运动时,运行轨道距离月球表面的高度为H,已知月球的质量为M,“嫦娥三号”的质量为m,月球半径为R月,引力常量G.忽略月球自转影响.求“嫦娥三号”在环月段上做匀速圆周运动时:(1)与月球之间的万有引力;
(2)运行速度;
(3)运行周期.
分析 (1)根据万有引力定律,即可求解;
(2)依据牛顿第二定律,结合万有引力提供向心力,列出$G\frac{Mm}{{{{({R_月}+H)}^2}}}=m\frac{v^2}{{{R_月}+H}}$表达式,即可求解;
(3)根据牛顿第二定律,结合万有引力提供向心力,列出$G\frac{Mm}{{{{({R_月}+H)}^2}}}=m{(\frac{2π}{T})^2}({R_月}+H)$表达式,即可求解.
解答 解:
(1)根据万有引力定律${F_万}=G\frac{Mm}{{{{({R_月}+H)}^2}}}$
(2)根据牛顿第二定律$G\frac{Mm}{{{{({R_月}+H)}^2}}}=m\frac{v^2}{{{R_月}+H}}$
解得$v=\sqrt{\frac{GM}{{{R_月}+H}}}$
(3)根据牛顿第二定律$G\frac{Mm}{{{{({R_月}+H)}^2}}}=m{(\frac{2π}{T})^2}({R_月}+H)$
解得 $T=2π\sqrt{\frac{{{{({R_月}+H)}^3}}}{GM}}$
答:(1)与月球之间的万有引力$\frac{GMm}{({R}_{月}+H)^{2}}$;
(2)运行速度$\sqrt{\frac{GM}{{R}_{月}+H}}$;
(3)运行周期$2π\sqrt{\frac{({R}_{月}+H)^{3}}{GM}}$.
点评 本题关键是要知道“嫦娥三号”绕月球做圆周运动的向心力由万有引力提供,并且要能够根据题目的要求选择恰当的向心力的表达式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.受“苹果落向地球”启发,某同学测得地球对苹果万有引力大小为2N,则( )
| A. | 苹果对地球不存在引力 | |
| B. | 苹果对地球存在引力大小为2N | |
| C. | 苹果对地球的引力忽略不计 | |
| D. | 地球对苹果的引力大于卫星对地球的引力 |
20. 一小球从光滑的斜面上的0点由静止开始向下运动,依次经过A、B、C、D、E五个点,已知AB=BC=CD=DE,物体经过B点时的速度vB和一小球从光滑的斜面上的0点由静止开始向下运动经过AE段的平均速度$\overline{v}$的大小关系是( )
一小球从光滑的斜面上的0点由静止开始向下运动,依次经过A、B、C、D、E五个点,已知AB=BC=CD=DE,物体经过B点时的速度vB和一小球从光滑的斜面上的0点由静止开始向下运动经过AE段的平均速度$\overline{v}$的大小关系是( )
 一小球从光滑的斜面上的0点由静止开始向下运动,依次经过A、B、C、D、E五个点,已知AB=BC=CD=DE,物体经过B点时的速度vB和一小球从光滑的斜面上的0点由静止开始向下运动经过AE段的平均速度$\overline{v}$的大小关系是( )
一小球从光滑的斜面上的0点由静止开始向下运动,依次经过A、B、C、D、E五个点,已知AB=BC=CD=DE,物体经过B点时的速度vB和一小球从光滑的斜面上的0点由静止开始向下运动经过AE段的平均速度$\overline{v}$的大小关系是( )| A. | vB<$\overline{v}$ | B. | vB=$\overline{v}$ | C. | vB>$\overline{v}$ | D. | 无法确定 |
17. 波源O沿y轴负方向开始振动形成一列沿x轴正方向传播的简谐横波,从O点起振开始计时,经t=0.7s,x轴上在0~10m的范围内第一次出现如图所示的波形,则( )
波源O沿y轴负方向开始振动形成一列沿x轴正方向传播的简谐横波,从O点起振开始计时,经t=0.7s,x轴上在0~10m的范围内第一次出现如图所示的波形,则( )
 波源O沿y轴负方向开始振动形成一列沿x轴正方向传播的简谐横波,从O点起振开始计时,经t=0.7s,x轴上在0~10m的范围内第一次出现如图所示的波形,则( )
波源O沿y轴负方向开始振动形成一列沿x轴正方向传播的简谐横波,从O点起振开始计时,经t=0.7s,x轴上在0~10m的范围内第一次出现如图所示的波形,则( )| A. | 此列波的波速为20m/s | |
| B. | 在t=0.7s时刻,质点A具有沿y轴负方向的最大加速度 | |
| C. | 此列波的周期为0.56s | |
| D. | 从质点A开始振动到t=0.7s,质点A通过的路程是0.3m |
4. 如图所示,一列简谐横波在介质中沿水平方向传播,实线是在t1=0时波的图象,虚线是在t2=0.5s时波的图象,已知介质中质点P在0~0.5s的时间内通过的路程为10cm.下面关于波的几个论述中正确的是( )
如图所示,一列简谐横波在介质中沿水平方向传播,实线是在t1=0时波的图象,虚线是在t2=0.5s时波的图象,已知介质中质点P在0~0.5s的时间内通过的路程为10cm.下面关于波的几个论述中正确的是( )
 如图所示,一列简谐横波在介质中沿水平方向传播,实线是在t1=0时波的图象,虚线是在t2=0.5s时波的图象,已知介质中质点P在0~0.5s的时间内通过的路程为10cm.下面关于波的几个论述中正确的是( )
如图所示,一列简谐横波在介质中沿水平方向传播,实线是在t1=0时波的图象,虚线是在t2=0.5s时波的图象,已知介质中质点P在0~0.5s的时间内通过的路程为10cm.下面关于波的几个论述中正确的是( )| A. | 简谐横波的波长为8m | B. | 波的传播方向水平向左 | ||
| C. | 波的传播速度为10m/s | D. | 波的频率为0.4Hz |
14. 如图所示,一根细绳的上端系在O点,下端系一个重球B,放在粗糙的斜面体A上.现用水平推力F向右推斜面体使之在光滑水平面上向右匀速运动一段距离(细绳尚未到达平行于斜面的位置).在此过程中以下判断不正确的是( )
如图所示,一根细绳的上端系在O点,下端系一个重球B,放在粗糙的斜面体A上.现用水平推力F向右推斜面体使之在光滑水平面上向右匀速运动一段距离(细绳尚未到达平行于斜面的位置).在此过程中以下判断不正确的是( )
 如图所示,一根细绳的上端系在O点,下端系一个重球B,放在粗糙的斜面体A上.现用水平推力F向右推斜面体使之在光滑水平面上向右匀速运动一段距离(细绳尚未到达平行于斜面的位置).在此过程中以下判断不正确的是( )
如图所示,一根细绳的上端系在O点,下端系一个重球B,放在粗糙的斜面体A上.现用水平推力F向右推斜面体使之在光滑水平面上向右匀速运动一段距离(细绳尚未到达平行于斜面的位置).在此过程中以下判断不正确的是( )| A. | 摩擦力对球B做正功 | |
| B. | 斜面对球B的弹力对小球做正功 | |
| C. | A对B所做的功与B对A所做的功大小相等 | |
| D. | 推力F和球B对A做功的大小相等 |
1.如图甲所示,一质量为M的长木板静置于光滑水平面上,其上放置一质量为m的小滑块.木板受到随时间t变化的水平拉力F作用时,用传感器测出长木板的加速度a与水平拉力F的关系如图乙所示,取g=10m/s2,则( )
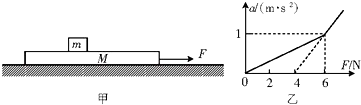

| A. | 小滑块的质量m=4kg | |
| B. | 当F=8 N时,滑块的加速度为2m/s2 | |
| C. | 滑块与木板之间的动摩擦因数为0.1 | |
| D. | 力随时间变化的函数关系一定可以表示为F=6t(N) |
18. 如图,在竖直平面内,直径为R的光滑半圆轨道和半径为R的光滑四分之一圆轨道水平相切于O点.O点在水平地面上.可视为质点的小球从O点以某一初速度进入半圆,刚好能通过半圆的最高点A,从A点飞出后落在四分之一圆轨道上的B点,不计空气阻力,g=10m/s2.则B点与A点的竖直高度差为( )
如图,在竖直平面内,直径为R的光滑半圆轨道和半径为R的光滑四分之一圆轨道水平相切于O点.O点在水平地面上.可视为质点的小球从O点以某一初速度进入半圆,刚好能通过半圆的最高点A,从A点飞出后落在四分之一圆轨道上的B点,不计空气阻力,g=10m/s2.则B点与A点的竖直高度差为( )
 如图,在竖直平面内,直径为R的光滑半圆轨道和半径为R的光滑四分之一圆轨道水平相切于O点.O点在水平地面上.可视为质点的小球从O点以某一初速度进入半圆,刚好能通过半圆的最高点A,从A点飞出后落在四分之一圆轨道上的B点,不计空气阻力,g=10m/s2.则B点与A点的竖直高度差为( )
如图,在竖直平面内,直径为R的光滑半圆轨道和半径为R的光滑四分之一圆轨道水平相切于O点.O点在水平地面上.可视为质点的小球从O点以某一初速度进入半圆,刚好能通过半圆的最高点A,从A点飞出后落在四分之一圆轨道上的B点,不计空气阻力,g=10m/s2.则B点与A点的竖直高度差为( )| A. | $\frac{(\sqrt{5}-1)R}{2}$ | B. | $\frac{(\sqrt{5}+1)R}{2}$ | C. | ($\sqrt{2}$-1)R | D. | ($\sqrt{2}$+1)R |
19.下列有关液晶的说法中正确的是( )
| A. | 液晶具有流动性 | |
| B. | 液晶具有各向异性 | |
| C. | 液晶的光学性质随所加压力的变化而变化 | |
| D. | 液晶就是液态的晶体 |