Question

【题目】如图，置于圆形水平转台边缘的小物块随转台缓慢加速转动，当转速达到某一数值时，物块恰好滑离转台开始做平抛运动．现测得转台半径R=0.5m，离水平地面的高度H=0.8m，物块与转台间的动摩擦因数μ=0.2．设物块所受的最大静摩擦力等于滑动摩擦力，取重力加速度g=10m/s2求：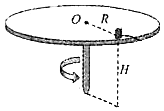

（1）物块做平抛运动的初速度大小v0；
（2）物块的落地点与转台的圆心O之间的水平距离．

Answer 1

【答案】
（1）解：最大静摩擦力刚好提供向心力时，则 ，解得v=

答：物块做平抛运动的初速度大小v0为1m/s

（2）物体离开平台后做平抛运动，下落的时间为t= ，水平通过的位移x=vt=0.4m

故物块的落地点与转台的圆心O之间的水平距离L=

答：物块的落地点与转台的圆心O之间的水平距离为 ．

【解析】（1）根据最大静摩擦力提供向心力求得平抛运动的初速度；（2）竖直方向做自由落体运动，求得时间，求得平抛运动的水平位移，根据几何关系求得距离
【考点精析】通过灵活运用平抛运动，掌握特点:①具有水平方向的初速度;②只受重力作用，是加速度为重力加速度g的匀变速曲线运动；运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动即可以解答此题．