��Ŀ����
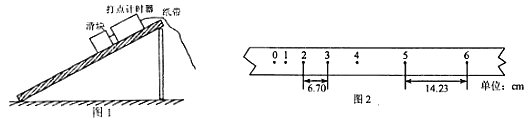
����Ŀ����ͼʾ������A����ˮƽ���ϣ�����ΪL=2m �� ��������mA=1kg��mB=0.99kg �� A��B��ֲڣ�����mC=0.01kg�ӵ���V0=200m/S�ٶ����һ���B���������У���![]()
��1���ӵ�C����B��˲�䣬B�ٶȶ��?
��2��������A��ˮƽ��̶���B���ӵ����к�ǡ�û���A�Ҷ˾�ֹ����B��A�䶯Ħ��������?
��3��������A��ˮƽ��⻬��B��A�䶯Ħ���������䣬�Է���B�ܷ��뿪����������������A��B��C��ɵ�ϵͳ��ʧ�Ļ�е�ܣ�
���𰸡�
��1��
�ӵ�����B�Ĺ�����ϵͳ�����غ㣬���ӵ��ij��ٶȷ���Ϊ������
�ɶ����غ㶨�ɵã������غ㣺mCv0=��mB+mC��v1���������ݽ�ã�v1=2m/S��
��2��
������A��ˮƽ��̶���B���˶�����ֹ��λ��ΪS�����ܶ����У�������mB+mC��gS=0�� ![]() ��mB+mC��v12���������ݽ�ã���=0.1��
��mB+mC��v12���������ݽ�ã���=0.1��
��3��
B��C��A���Ħ������F=����mB+mC��g���������ݽ�ã�F=1N��
ϵͳ�����غ㣬��AB�ij��ٶȷ���Ϊ�������ɶ����غ㶨�ɵã�
��mB+mC��v1=��mA+mB+mC��v2���������ݽ�ã�v2=1m/S��
��ʱB���Aλ��ΪS�䣬�������غ㶨�ɵģ����ܹ�ϵ֪��
![]() ��mB+mC��v12=
��mB+mC��v12= ![]() ��mA+mB+mC��v22+FS�䣬�������ݽ�ã�S��=1m��
��mA+mB+mC��v22+FS�䣬�������ݽ�ã�S��=1m��
��S�䣼L��A��B��C������˶���������룬
�������غ㶨�ɵã�ϵͳ��ʧ�Ļ�е��Ϊ��Q= ![]() mCv02��
mCv02�� ![]() ��mA+mB+mC��v22��
��mA+mB+mC��v22��
�������ݽ�ã�Q=199J
����������1���ӵ�����B�Ĺ���ϵͳ�����غ㣬�ɶ����غ㶨�ɿ������B���ٶȣ���2���ɶ��ܶ������������Ħ����������3��Ӧ�ö����غ㶨���������غ㶨�ɷ������⣮
�����㾫����������Ŀ����֪���������ö����غ㶨�ɵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ն����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��䣮