题目内容
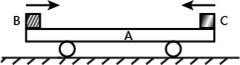
(12分)如图所示为某工厂将生产工件装车的流水线原理示意图。设AB段是距水平传送带装置高为H=1.25m的光滑曲面,水平段BC使用水平传送带装置传送工件,工件经C点抛出后落在固定车厢中。已知BC长L=3m,工件可视为质点,传送带与工件间的动摩擦因数为μ=0.4。设质量m=lkg的工件由静止开始从A点下滑,经过B点的拐角处无机械能损失,取g= l0m/s2。求:
(1)当传送带静止时,工件运动到C点时的速度是多大?
(2)当传送带以v=8m/s顺时针方向匀速转动时,在工件运动到C点的过程中因摩擦而产生的内能是多少?
(1)1m/s (2)4J
解析试题分析:(1)设工件质量为m,当皮带静止时,工件从A运动至C过程,
根据动能定理有 mgH-µmgL=mvc2/2-0
代入数据解得:vc=1m/s
(2) 工件从A运动至B过程,根据动能定理有
mgH=mvB2/2-0
解得vB=5m/s
当皮带以v=8m/s顺时针方向匀速转动时,工件先做匀加速运动
对工件根据牛顿第二定律有µmg=ma a= µg=4m/s2
设工件速度加速到皮带速度v=8m/s相同时,经过的时间为t
v-vB=at t=0.75s
在t时间内工件对地的位移工件 4.875m>3m,说明工件在传送带上全程都是被加速。
4.875m>3m,说明工件在传送带上全程都是被加速。
或利用 得
得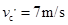 <8m/s,说明工件在传送带上全程都是被加速。
<8m/s,说明工件在传送带上全程都是被加速。
设工件在传送带上实际被加速的时间为t1,
代入数据解得:t1=0.5s (另一解t1=-3s舍去)
或利用 ,代入数据解得:t1=0.5s
,代入数据解得:t1=0.5s
在t1时间传送带对地的位移为s,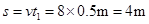
工件相对于传送带的位移 ,
,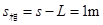
由功能关系可知:由摩擦产生的内能
考点:本题考查动能定理、牛顿第二定律、运动学关系和摩擦生热的计算方法的掌握。

练习册系列答案
相关题目


 =O.8 m,质量M=12 kg,在牵引力为零时,仍在向前运动。车与路面的动摩擦因数为O.3,当车速为
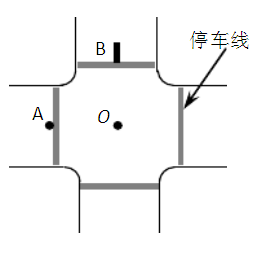
=O.8 m,质量M=12 kg,在牵引力为零时,仍在向前运动。车与路面的动摩擦因数为O.3,当车速为 =7 m/s时,把一个质量为m=1 kg的物体(可视为质点)轻轻地放在车顶前端,如图所示,问物体落地时,物体距车的前端有多远?(g=10m/s2)
=7 m/s时,把一个质量为m=1 kg的物体(可视为质点)轻轻地放在车顶前端,如图所示,问物体落地时,物体距车的前端有多远?(g=10m/s2)
