��Ŀ����
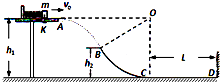
����Ŀ����ͼ��ʾ��Ħ�г����ؼ�����ʱ����v0=10m/s�ij��ٶȳ����̨��Ȼ��Ӹ�̨ˮƽ�ɳ�����Ħ�г������̨�Ĺ�������P=1.8kW�Ķ������ʻ���嵽��̨������ʱ��t=16s���˺ͳ���������m=1.8��102kg��̨��h=5.0m��Ħ�г�����ص㵽��̨��ˮƽ����s=7.5m�����ƿ���������ȡg=10m/s2 �� ��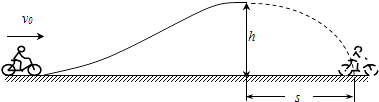
��1��Ħ�г��Ӹ�̨�ɳ����������ʱ�䣻
��2��Ħ�г����ʱ�ٶȵĴ�С��
��3��Ħ�г����ϸ�̨�����п˷����������Ĺ���
���𰸡�
��1���⣺Ħ�г��ڿ�����ƽ���˶�
���� ![]() s
s
��Ħ�г��Ӹ�̨�ɳ����������ʱ��Ϊ1s��
��2���⣺ˮƽ�������˶��˶������У� ![]() m/s
m/s
��ֱ���������������˶�����v��ֱ=gt
���v��ֱ=10m/s
Ħ�г����ʱ���ٶȣ� ![]() m/s
m/s
��Ħ�г����ʱ�ٶȵĴ�СΪ12.5m/s��
��3���⣺Ħ�г����ϸ�̨�����У����ݶ��ܶ�����
![]()
�������ݵã�
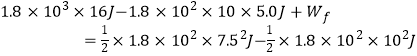
��ã� ![]()
���ԣ�Ħ�г����ϸ�̨������Ħ�г��˷����������Ĺ�Ϊ2.4��104J
��Ħ�г����ϸ�̨�����п˷����������Ĺ�Ϊ2.4��104J��
����������1��ƽ���˶���ʱ���ɸ߶Ⱦ���������h= ![]() ����˶���ʱ�䣮��2���ֱ����ˮƽ�������ֱ�����ϵķ��ٶȣ�����ƽ���ı��ζ��������ص��ٶȴ�С����3��ץס���ʲ��䣬ǣ��������W=Pt�����ݶ��ܶ������Ħ�г����ϸ�̨�����п˷����������Ĺ���
����˶���ʱ�䣮��2���ֱ����ˮƽ�������ֱ�����ϵķ��ٶȣ�����ƽ���ı��ζ��������ص��ٶȴ�С����3��ץס���ʲ��䣬ǣ��������W=Pt�����ݶ��ܶ������Ħ�г����ϸ�̨�����п˷����������Ĺ���
�����㾫����������Ҫ������ƽ���˶��Ͷ��ܶ������ۺ�Ӧ�õ����֪ʶ�㣬��Ҫ�����ص�:�پ���ˮƽ����ij��ٶ�;��ֻ���������ã��Ǽ��ٶ�Ϊ�������ٶ�g���ȱ��������˶����˶�����:ƽ���˶����Էֽ�Ϊˮƽ���������ֱ���˶�����ֱ��������������˶���Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݲ�����ȷ�����⣮

 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д�