题目内容
【题目】质量为m的物块，沿着半径为R的半球形金属壳内壁滑下，半球形金属壳竖直放置，开口向上，滑到最低点时速度大小为v，若物体与球壳之间的摩擦因数为μ，则物体在最低点时，下列说法正确的是（ ）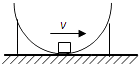
A.受到向心力为 
B.受到的摩擦力为 
C.受到的摩擦力为μmg
D.受到的合力方向斜向左上方
【答案】D
【解析】解：A、物体滑到半球形金属球壳最低点时，速度大小为v，半径为R，向心加速度为an= 
，故A错误；
B、根据牛顿第二定律得N﹣mg=m ，得到金属球壳对小球的支持力N=m（g+ ），由牛顿第三定律可知，小球对金属球壳的压力大小N′=m（g+ ），受到的摩擦力为f=μN=μm（g+ ），故BC错误；
D、物体重力和支持力的合力向上，还受到水平向左的摩擦力，属于物体受到的合力方向斜向左上方，故D正确．
故选：D
【考点精析】本题主要考查了向心力的相关知识点，需要掌握向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力才能正确解答此题．
练习册系列答案
相关题目
