题目内容
【题目】如图所示,在平面直角坐标系xoy中的有一个等腰直角三角形硬质细杆框架FGH,框架竖直放在粗糙的水平面上,其中FG与地面接触。空间存在着垂直于框架平面的匀强磁场,磁感应强度为B,FG的长度为8L,在框架底边FG中垂线OH上S(0,L)处有一体积可忽略的粒子发射装置,在该平面内向各个方向发射速度大小相等且带正电的大量同种粒子,射到框架上的粒子立即被框架吸收.粒子的质量为m,电荷量为q,不计粒子间的相互作用以及粒子的重力.
(1)试问速率在什么范围内所有粒子均不可能打到框架上?
(2)如果粒子的发射速率
,求出框架上能被粒子打中的长度
(3)如果粒了的发射速率仍为
,某时刻同时从S点发出粒子,求从第一个粒子到达底边FG至最后一个到达底边的时间间隔△t.
【答案】（1）
（2）
（3）
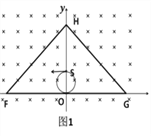
【解析】（1）如图1所示，以OS为直径的粒子在运动过程中刚好不碰到框架上。
根据几何关系， 
根据牛顿第二定律
可得满足
的粒子均不可能碰到三角形框架．
（2）当粒子速率
时，可求得其做圆周运动半径
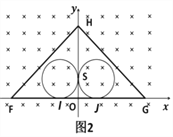
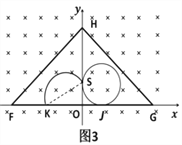
如图2所示，当粒子的入射速度方向沿SO方向时，运动轨迹与FG相切于J点；当粒子的入射速度方向沿OS时，运动轨迹与FG相切于I点，速度方向介于这二者之间的入射粒子均可打在挡板FG上，挡板上被粒子打中的长度为图3中JK之间的距离，其中
SK=2r=2L， 
挡板上被粒子打中的长度
（3）通过分析最长时间为
， 最短时间为
，而
故
练习册系列答案
53天天练系列答案
相关题目
