题目内容
(20分)如图所示,x轴正方向水平向右,y轴正方向竖直向上。在xOy平面内有与y轴平行的匀强电场,在半径为R的圆内还有与xOy平面垂直的匀强磁场。在圆的左边放置一带电微粒发射装置,它沿x轴正方向发射出一束具有相同质量m、电荷量q(q>0)和初速度v的带电微粒。发射时,这束带电微粒分布在0<y<2R的区间内。已知重力加速度大小为g。

(1)从A点射出的带电微粒平行于x轴从C点进入有磁场区域,并从坐标原点O沿y轴负方向离开,求电场强度和磁感应强度的大小和方向。
(2)请指出这束带电微粒与x轴相交的区域,并说明理由。
(3)若这束带电微粒初速度变为2v,那么它们与x轴相交的区域又在哪里?并说明理由。

(1)从A点射出的带电微粒平行于x轴从C点进入有磁场区域,并从坐标原点O沿y轴负方向离开,求电场强度和磁感应强度的大小和方向。
(2)请指出这束带电微粒与x轴相交的区域,并说明理由。
(3)若这束带电微粒初速度变为2v,那么它们与x轴相交的区域又在哪里?并说明理由。
(1) ,方向沿y轴正方向。
,方向沿y轴正方向。 ,方向垂直xOy平面向外。
,方向垂直xOy平面向外。
(2)这束带电微粒都是通过坐标原点后离开磁场的。理由见解析。
(3)这束带电微粒与x轴相交的区域范围是 。
。
 ,方向沿y轴正方向。
,方向沿y轴正方向。 ,方向垂直xOy平面向外。
,方向垂直xOy平面向外。(2)这束带电微粒都是通过坐标原点后离开磁场的。理由见解析。
(3)这束带电微粒与x轴相交的区域范围是
 。
。(1)带电微粒平行于x轴从C点进入磁场,说明带电微粒所受重力和电场力的大小相等,方向相反。设电场强度大小为E,由
mg=qE
可得电场强度大小

方向沿y轴正方向。
带电微粒进人磁场后受到重力、电场力和洛仑兹力的作用。由于电场力和重力相互抵消,它将做匀速圆周运动。如图(a)所示,考虑到带电微粒是从C点水平进入磁场,过O点后沿y轴负方向离开磁场,可得圆周运动半径
r=R
设磁感应强度大小为B,由
 可得磁感应强度大小
可得磁感应强度大小 方向垂直xOy平面向外。
方向垂直xOy平面向外。
(2)这束带电微粒都通过坐标原点。
理由说明如下:
方法一:从任一点P水平进人磁场的带电微粒在磁场中做半径为R的匀速圆周运动,其圆心位于其正下方的Q点,如图(b)所示。这样,这束带电微粒进入磁场后的圆心轨迹是如图所示的虚线半圆,此半圆的圆心是坐标原点。所以,这束带电微粒都是通过坐标原点后离开磁场的。
方法二:从任一点P水平进入磁场的带电微粒在磁场中做半径为R的匀速圆周运动。如图(b)所示,设P点与0´点的连线与y轴的夹角为
 ,其圆周运动的圆心Q的坐标为(-Rsin
,其圆周运动的圆心Q的坐标为(-Rsin ,Rcos
,Rcos ),圆周运动轨迹方程为
),圆周运动轨迹方程为
而磁场边界是圆心坐标为(0,R)的圆周,其方程为

解上述两式,可得带电微粒做圆周运动的轨迹与磁场边界的交点为
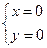 或
或
坐标为(-Rsin
 ,R(1+cos
,R(1+cos ))的点就是P点,须舍去。由此可见,这束带电微粒都是通过坐标原点后离开磁场的。
))的点就是P点,须舍去。由此可见,这束带电微粒都是通过坐标原点后离开磁场的。(3)这束带电微粒与x轴相交的区域是x>0。
理由说明如下:
带电微粒初速度大小变为2v,则从任一点P水平进入磁场的带电微粒在磁场中做匀速圆周运动的半径r´为
r´=

带电微粒在磁场中经过一段半径为
 的圆弧运动后,将在
的圆弧运动后,将在 轴的右方(
轴的右方( 区域)离开磁场并做匀速直线运动,如图(c)所示。靠近
区域)离开磁场并做匀速直线运动,如图(c)所示。靠近 点发射出来的带电微粒在穿出磁场后会射向x轴正方向的无穷远处:靠近
点发射出来的带电微粒在穿出磁场后会射向x轴正方向的无穷远处:靠近 点发射出来的带电微粒会在靠近原点之处穿出磁场。
点发射出来的带电微粒会在靠近原点之处穿出磁场。所以,这束带电微粒与x轴相交的区域范围是
 。
。

练习册系列答案
相关题目
 ,电子的重力忽略不计,求:
,电子的重力忽略不计,求:
 ,电子的质量为m,电荷量大小为e,电子重力和进入两板间初速度可以忽略.求:
,电子的质量为m,电荷量大小为e,电子重力和进入两板间初速度可以忽略.求:


 。
。
 =2.30V,网板上方为垂直纸面大小为6.28×
=2.30V,网板上方为垂直纸面大小为6.28× T的匀强磁场,P与S正对.设想在某一时刻,一个自由电子从P点由静止开始运动,并穿过网板最后到达S',已知SS'相距3.27×
T的匀强磁场,P与S正对.设想在某一时刻,一个自由电子从P点由静止开始运动,并穿过网板最后到达S',已知SS'相距3.27× m,设自由电子始终不会被吸附,整个装置放在真空中.求该自由电子从P第一次到达S'所需的时间.(电子荷质比e/m=1.76×
m,设自由电子始终不会被吸附,整个装置放在真空中.求该自由电子从P第一次到达S'所需的时间.(电子荷质比e/m=1.76× C/kg)
C/kg)