题目内容
【题目】宇宙间存在一些离其他恒星较远的、由质量相等的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.已观测到的四星系统存在着一种基本的构成形式是:三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆形轨道运行,第四颗星位于圆形轨道的圆心处,已知引力常量为G,圆形轨道的半径为R,每颗星体的质量均为m.求:
(1)中心星体受到其余三颗星体的引力的合力大小;
(2)三颗星体沿圆形轨道运动的线速度和周期.
【答案】(1)零(2)![]() (3)
(3)![]()
【解析】本题考查多星问题,涉及环绕星体的受力分析、环绕星体运动速度和周期的计算。
(1) 四星系统的圆周运动示意图如图所示

中心星体受到其余三颗星体的引力大小相等,方向互成120°.
根据力的合成法则,中心星体受到其他三颗星体的引力的合力为零.
(2) 对圆形轨道上任意一颗星体,根据万有引力定律和牛顿第二定律有![]() ,
,![]()
解得三颗星体沿圆形轨道运动的线速度![]()
三颗星体运动的周期![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在探究小车的加速度a与小车质量M和小车受到的外力F的关系时,
(1)探究加速度和力的关系的实验数据描绘出的a-F图象如图所示,下列说法正确的是________(填正确答案标号)。
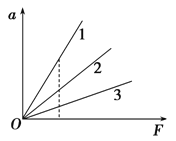
A.三条倾斜的直线所对应的小车的质量相等 |
B.三条倾斜的直线所对应的小车的质量不同 |
C.直线1所对应的小车的质量最大 |
D.直线3所对应的小车的质量最大 |
(2)由于没有始终满足小车的质量M远大于钩码的质量m的关系,结果得到的图象应是下图中的________(填正确答案标号)。