题目内容
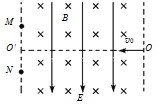
【题目】如图所示,滑板轨道BC为竖直平面内的四分之一圆弧赛道,半径为R=1.8 m。ABC为光滑轨道,且水平轨道AB与圆弧轨道BC在B点相切。若运动员的质量M=48.0 kg,滑板质量m=2.0 kg,二者均可视为质点,重力加速度g取10 m/s2,不计空气阻力。
(1)运动员和滑板在A点的速度至少多大才能滑到C点?
(2)以第(1)问中的最小速度运动时,求运动员滑过圆弧形轨道B点时对轨道的压力;
(3)若A点右侧为动摩擦因数μ=0.3的水泥地面,运动员以第(1)问中的最小速度滑至C点又滑回后,运动员与滑板会停在距A点多远的位置?

【答案】(1)6.0 m/s (2)1.5×103 N (3)6.0 m
【解析】(1)以运动员和滑板为一整体,若运动员和滑板恰好可滑到C点,以A、B所在水平面为零势面,由机械能守恒定律得
![]() (m+M)v2=(m+M)gR
(m+M)v2=(m+M)gR
解得v=6.0 m/s
运动员和滑板在A点的速度v至少要达到6.0 m/s才能滑到C点
(2)以第(1)问中的最小速度v运动时,由牛顿第二定律得
FN-(m+M)g=![]()
解得轨道对运动员和滑板的支持力为FN=1.5×103 N
由牛顿第三定律可知运动员和滑板对轨道的压力大小也等于1.5×103 N,方向向下
(3)因为轨道ABC光滑,由机械能守恒定律知运动员滑回A点时速度大小仍为v=6.0 m/s
滑过A点后至停下的过程可由动能定理得
-μ(m+M)gx=0-![]() (m+M)v2
(m+M)v2
代入数据解得运动员和滑板最后与A点的距离为x=6.0 m。

练习册系列答案
相关题目