题目内容
真空中的光滑水平绝缘面上有一带电小滑块,开始时滑块静止。若在滑块所在空间加一水平匀强电场E1,持续一段时间后立刻换成与E1相反方向的匀强电场E2。当电场E2与电场E1持续时间相同时,滑块恰好回到初始位置,且具有动能EK。在上述过程中,E1对滑块的电场力做功为W1,冲量大小为I1;E2对滑块的电场力做功为W2,冲量大小为I2。则 ( )
| A.I1=I2 | B.4I1=I2 |
| C.W1=0.25Ek,W2="0.75" Ek | D.W1=0.20Ek,W2="0.80" Ek |
C
根据题目给条件,构建如下的物理情景(假设滑块带正电,若滑块带负电,分析方法相同),如图答1所示。根据物理情景,本题属于求解恒力做功和恒力冲量的问题。一般有两种方法:一是利用功的定义和冲量的定义求解——需先求得两个过程中的电场强度,继而求得两个过程的电场力,即可求得功和冲量;二是利用动能定理和动量定理求解,除了需先求得以上的物理量之外,还需求得两个过程的末速度。


解法一:用力和运动的观点
前t内:小滑块做匀加速直线运动 ,
, ,
, ;
;
后t内:小滑块做类竖直上抛运动,则根据题意有:
 ,
,
解以上各式可得:
所以,所受电场力冲量的大小
电场力所做的功 又
又
可解得: ,
,
正确选项为C
解法二: 用动能和动量的观点
设前、后两过程的末速度大小为 和
和 ,位移大小为s,根据动能定理和动量定理有:
,位移大小为s,根据动能定理和动量定理有:
前t内:

后t内:

解以上四式得: (以下同解法一)
(以下同解法一)
解法三:用运动学公式和动量定理与动能定理
设前、后两过程的末速度大小为 和
和 ,由题意可知,前后两个过程的平均速度大小相等,则:
,由题意可知,前后两个过程的平均速度大小相等,则: ,于是可得:
,于是可得:
根据动量定理可得: ,
,
根据动能定理得: ,
,
(以下解法同解法一)
解法四:用图象法和动量定理与动能定理
画出小滑块的v-t图象(如图答2所示),由题意知物体总位移为零,则面积:
又在后t时间内加速度相等,于是斜率:
 由以上二式可解得:
由以上二式可解得:
(以下解法同解法三)
命题思路: (1)本题考查电场力作用下的力和运动问题、冲量、动量定理、动能定理、电场力做功的特点及计算等知识,同时考查分析能力和综合应用知识的能力。解题的关键是明确带电滑块运动的物理过程,画出过程图;(2)比较以上四种解法,侧重点不一样,有的简单、有的巧妙,各有特色;(3)通过该题的求解,说明物理基础知识的重要性。因此,学习时不但要注重重点知识和主干知识,更要掌握基础知识。


解法一:用力和运动的观点
前t内:小滑块做匀加速直线运动
 ,
, ,
, ;
;后t内:小滑块做类竖直上抛运动,则根据题意有:

 ,
,
解以上各式可得:

所以,所受电场力冲量的大小

电场力所做的功
 又
又
可解得:
 ,
,
正确选项为C
解法二: 用动能和动量的观点
设前、后两过程的末速度大小为
 和
和 ,位移大小为s,根据动能定理和动量定理有:
,位移大小为s,根据动能定理和动量定理有:前t内:


后t内:


解以上四式得:
 (以下同解法一)
(以下同解法一)解法三:用运动学公式和动量定理与动能定理
设前、后两过程的末速度大小为
 和
和 ,由题意可知,前后两个过程的平均速度大小相等,则:
,由题意可知,前后两个过程的平均速度大小相等,则: ,于是可得:
,于是可得:
根据动量定理可得:
 ,
,
根据动能定理得:
 ,
,
(以下解法同解法一)
解法四:用图象法和动量定理与动能定理
画出小滑块的v-t图象(如图答2所示),由题意知物体总位移为零,则面积:

又在后t时间内加速度相等,于是斜率:
 由以上二式可解得:
由以上二式可解得:
(以下解法同解法三)
命题思路: (1)本题考查电场力作用下的力和运动问题、冲量、动量定理、动能定理、电场力做功的特点及计算等知识,同时考查分析能力和综合应用知识的能力。解题的关键是明确带电滑块运动的物理过程,画出过程图;(2)比较以上四种解法,侧重点不一样,有的简单、有的巧妙,各有特色;(3)通过该题的求解,说明物理基础知识的重要性。因此,学习时不但要注重重点知识和主干知识,更要掌握基础知识。

练习册系列答案
相关题目

 垂直于电场方向射入场强为E的匀强电场中,穿出电场区域时偏转角为
垂直于电场方向射入场强为E的匀强电场中,穿出电场区域时偏转角为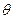 。在同样的宽度范围内,若改用方向垂直于纸面向里的匀强磁场,使该离子穿过磁场区域时偏转角也为
。在同样的宽度范围内,若改用方向垂直于纸面向里的匀强磁场,使该离子穿过磁场区域时偏转角也为



 角,现突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其他影响(重力加速度为g),求:
角,现突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其他影响(重力加速度为g),求:

 ,
, 粒子经历时间为
粒子经历时间为 ,则
,则