题目内容
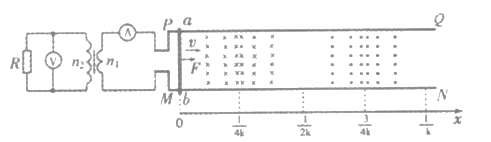
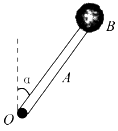
【题目】如图所示为一简化后的跳台滑雪的雪道示意图，运动员从O点由静止开始，在不借助其它外力的情况下，自由滑过一段圆心角为60°的光滑圆弧轨道后从A点水平飞出，然后落到斜坡上的B点。已知A点是斜坡的起点，光滑圆弧轨道半径为40m，斜坡与水平面的夹角θ＝30°，运动员的质量m＝50 kg，重力加速度g＝10 m／s2。下列说法正确的是
A. 运动员从O运动到B的整个过程中机械能守恒
B. 运动员到达A点时的速度为20 m／s
C. 运动员到达B点时的动能为10 kJ
D. 运动员从A点飞出到落到B点所用的时间为
s
【答案】AB
【解析】运动员在光滑的圆轨道上的运动和随后的平抛运动的过程中只受有重力做功，机械能守恒．故A正确；运动员在光滑的圆轨道上的运动的过程中机械能守恒，所以：
mvA2=mgh=mgR（1-cos60°）所以：
，故B正确；设运动员做平抛运动的时间为t，则：x=vAt；y=gt2
由几何关系：
，联立得：
，
运动员从A到B的过程中机械能守恒，所以在B点的动能：EkB=mgy+mvA2，代入数据得：EkB=
×105J．故C D错误．故选AB.
点睛：本题是常规题，关键要抓住斜面的倾角反映位移的方向，知道平抛运动水平方向做匀速直线运动，竖直方向做自由落体运动，难度适中.
【题型】多选题
【结束】
88
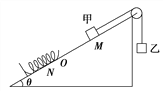
【题目】如图所示，在倾角为30°的斜面上固定一电阻不计的光滑平行金属导轨，其间距为L，下端接有阻值为R的电阻，导轨处于匀强磁场中，磁感应强度大小为B，方向与斜面垂直(图中未画出)。质量为m、阻值大小也为R的金属棒ab与固定在斜面上方的劲度系数为k的绝缘弹簧相接，弹簧处于原长并被锁定。现解除锁定的同时使金属棒获得沿斜面向下的速度v0，从开始运动到停止运动的过程中金属棒始终与导轨垂直并保持良好接触，弹簧始终在弹性限度内，重力加速度为g，在上述过程中( )
A. 开始运动时金属棒与导轨接触点间电压为
B. 通过电阻R的最大电流一定是
C. 通过电阻R的总电荷量为
D. 回路产生的总热量小于
【答案】AD
【解析】开始运动时，产生的电动势E=BLv0，金属棒与导轨接触点间电压为路端电压
，所以A正确；开始运动时，导体棒受重力mg、安培力BIL、支持力FN，若mg大于BIL，则导体棒加速运动，速度变大，电动势增大，电流增大，即最大电流大于
，所以B错误；最后静止时，
，过电阻R的总电荷量为
，所以C错误；全程利用能量守恒：
，所以产生的热量
，EP为弹性势能，故D正确。
