题目内容
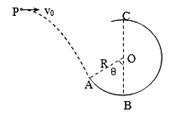
如图所示，AB为半径R＝0.8 m的1/4光滑圆弧轨道，下端B恰与小车右端平滑对接．小车质量M＝3 kg，车长L＝2.06 m，车上表面距地面的高度h＝0.2 m．现有一质量m＝1 kg的滑块，由轨道顶端无初速释放，滑到B端后冲上小车．已知地面光滑，滑块与小车上表面间的动摩擦因数μ＝0.3，当车运行了1.5 s时，车被地面装置锁定．(g＝10 m/s2)试求：
(1)滑块刚到达B端瞬间，轨道对它支持力的大小；
(2)车被锁定时，车右端距轨道B端的距离；
(3)从车开始运动到被锁定的过程中，滑块与车面间由于摩擦而产生的内能大小；
(4)滑块落地点离车左端的水平距离．
(1)30 N (2)1 m (3)6 J (4)0.16 m
解析试题分析：解析：(1)设滑块到达B端时速度为v，
由动能定理，得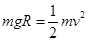
由牛顿第二定律，得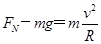
联立两式，代入数值得轨道对滑块的支持力：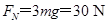
.
(2)当滑块滑上小车后，由牛顿第二定律，得
对滑块有：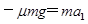
对小车有：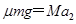
设经时间t两者达到共同速度，则有：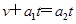
解得t＝1s．由于1s＜1.5 s，此时小车还未被锁定，两者的共同速度：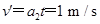
因此，车被锁定时，车右端距轨道B端的距离：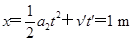
.
(3)从车开始运动到被锁定的过程中，滑块相对小车滑动的距离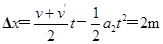
所以产生的内能：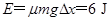
.
(4)对滑块由动能定理，得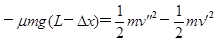
滑块脱离小车后，在竖直方向有：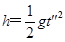
所以，滑块落地点离车左端的水平距离：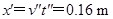
.
考点：力学综合问题
点评：本题涉及到机械能守恒、竖直平面内圆周运动、牛顿第二定律、运动学公式、动能定理、功能关系、平抛运动等重要知识点，是一道典型的力学综合问题。
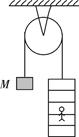
如图所示，竖直光滑杆上套一个小球和两根弹簧，两弹簧的一端各与小球相连，另一端分别用销钉M、N固定于杆上，小球处于静止状态。设拔去销钉M瞬间，小球加速度的大小为12m/s2。若不拔去销钉M而拔去销钉N瞬间，小球的加速度可能是（取g=10m/s2）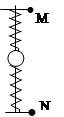
| A．22m/s2，竖直向上 | B．22m/s2，竖直向下 | C．2m/s2，竖直向上 | D．2m/s2，竖直向下 |
，
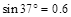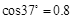。求：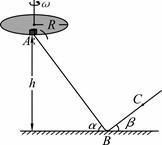
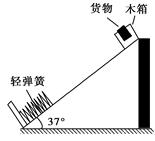
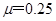.设计要求：木箱在轨道顶端时，自动装货装置将质量
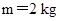的货物装入木箱，木箱载着货物沿轨道无初速滑下，当轻弹簧被压缩至最短时，自动装货装置立刻将货物卸下，然后木箱恰好被弹回到轨道顶端，接着再重复上述过程．若g取
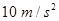，sin 37°＝0.6 ，cos 37°＝0.8.求：
如图，人站在楼梯的水平踏板上静止不动，以下表述正确的是 
| A．人受到重力和踏板对人的支持力是一对作用力和反作用力 |
| B．人对踏板的压力和踏板对人的支持力是一对平衡力 |
| C．人受到重力和支持力的作用 |
| D．人受到重力、支持力和静摩擦力的作用 |
