题目内容
（10分）如图，一个质量为0.6kg 的小球以某一初速度从P点水平抛出，恰好从光滑圆弧ABC的A点的切线方向进入圆弧（不计空气阻力，进入圆弧时无机械能损失）。已知圆弧的半径R=0.3m，θ=60°，小球到达A点时的速度 vA="4" m/s 。取g ="10" m/s2，求：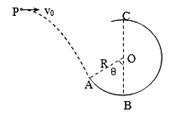
（1）小球做平抛运动的初速度v0；
（2）P点与A点的高度差；
（3）小球到达圆弧最高点C时对轨道的压力。
(1)v0="2" m/s (2)h="0.6m" (3)NC=8N
解析
试题分析：(1) 由题意知小球到A点的速度
沿曲线A点的切线方向，,对速度分解如图所示，小球做平抛运动，由平抛运动规律得
m/s，所以小球做平抛运动的初速度v0 ="2" m/s。
(2) 
m/s，
由平抛运动规律得：
，解得：h="0.6" m，P点与A点的高度差0.6m。
(3) 从A点到C点的过程中，由机械能守恒定律
，解得
m/s
小球在C点由圆周运动的向心力公式得：NC+mg=m
代入数据得：NC="8" N
由牛顿第三定律得：小球对轨道的压力大小NC'= NC=8N，方向竖直向上
考点：平抛运动规律 机械能守恒定律 牛顿第三定律
名校课堂系列答案
在春天，河水边上的湿地是松软的，人在这些湿地上行走时很容易下陷，此时( )
| A．人对湿地地面的压力大于湿地地面对他的支持力 |
| B．人对湿地地面的压力等于湿地地面对他的支持力 |
| C．人对湿地地面的压力小于湿地地面对他的支持力 |
| D．无法确定 |
如图所示，静止的弹簧测力计受到大小都为40N的F1，F2的作用，弹簧测力计的示数为( )
| A．0N | B．40N | C．80N | D．无法确定 |
如图所示，用细绳把小球悬挂起来，当小球静止时，下列说法中正确的是（ ）
| A．小球受到的重力和细绳对小球的拉力是一对作用力和反作用力 |
| B．小球受到的重力和小球对细绳的拉力是一对作用力和反作用力 |
| C．小球受到的重力和细绳对小球的拉力是一对平衡力 |
| D．小球受到的重力和小球对细绳的拉力是一对平衡力 |
某跳水运动员在3m长的踏板上起跳，我们通过录像观察到踏板和运动员要经历如图所示的状态，其中A为无人时踏板静止点，B为人站在踏板上静止时的平衡点，C为人在起跳过程中人和踏板运动的最低点，则下列说法中正确的是（ ）
| A．人和踏板由C到B的过程中，人向上做匀加速运动 |
| B．人和踏板由C到A的过程中，人处于超重状态 |
| C．人和踏板由C到A的过程中，先超重后失重 |
| D．人在C点具有最大速度 |
一物体静止在地面上，在竖直方向的拉力作用下开始向上运动（不计空气阻力）．在向上运动的过程中，以地面为参考平面，物体的机械能E与上升高度h的关系图象如图7所示，其中0-h1过程的图线是过原点的直线，h1~h2过程的图线为平行于横轴的直线．则
| A．在0~h2上升过程中，物体先做加速运动，后做匀速运动 |
| B．在0~h1上升过程中，物体的加速度不断增大 |
| C．在0~hl上升过程中，拉力的功率保持不变 |
| D．在h1~h2上升过程中，物体处于完全失重状态 |
对于超重和失重的认识，以下正确的是( )
| A．人站在体重计时，突然下蹲，体重计示数不变 |
| B．蹦床运动员在上升到最高点时处于平衡状态 |
| C．在减速上升的电梯里人对地板的压力小于重力 |
| D．跳水运动员被跳板弹起，离开跳板向上运动是超重现象 |
