题目内容
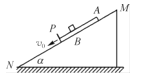
【题目】如图所示,在水平地面同一直线上分别固定一个![]() 圆环轨道和一个倾角为
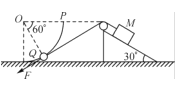
圆环轨道和一个倾角为![]() 的斜面。OP为圆环轨道的水平半径,斜面顶端固定一大小忽略的轻滑轮且与OP在同一水平高度。一轻绳跨过定滑轮左端与套圆环轨道上质量为m的小圆环相连,右端与斜面上质量为M的物块相连。小圆环在沿Q点切线向下的外力作用下静止于Q点,轻绳恰好也与轨道相切,OQ、OP间夹角为
的斜面。OP为圆环轨道的水平半径,斜面顶端固定一大小忽略的轻滑轮且与OP在同一水平高度。一轻绳跨过定滑轮左端与套圆环轨道上质量为m的小圆环相连,右端与斜面上质量为M的物块相连。小圆环在沿Q点切线向下的外力作用下静止于Q点,轻绳恰好也与轨道相切,OQ、OP间夹角为![]() 。撤去外力后小圆环运动到P点的速度恰好为零。忽略一切摩擦阻力,小圆环和物块均可视为质点,物块离斜面底端足够远,重力加速度为g。求:
。撤去外力后小圆环运动到P点的速度恰好为零。忽略一切摩擦阻力,小圆环和物块均可视为质点,物块离斜面底端足够远,重力加速度为g。求:
(1)外力F的大小;
(2)小圆环与物块质量的比值![]() ;
;
(3)当小圆环再次向下运动到Q点时,轻绳张力T的大小(结果用m、g表示)。
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) 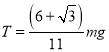
【解析】
(1)对小圆环受力分析,由平衡条件可得在沿Q点切线方向上有
![]()
![]()
解得![]()
(2)当小圆环运动到P点速度恰好为0时,物块M的速度也为0。设圆弧半径为R,此过程中小圆环上升的高度
![]()
物块M沿斜面下滑距离为
![]()
由机械能守恒定律可得
![]()
解得![]()
(3)当小圆环再次滑到Q点时,由牛顿第二定律得对物块有
![]()
对小圆环在Q点切线方向上有
![]()
解得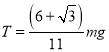

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目