��Ŀ����
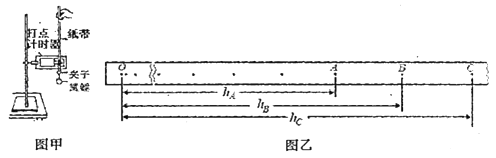
����Ŀ����ͼ��ʾ����Դ�綯��E��2 V���ڵ���r��0.5 ������ֱ�������ɺ��ԣ�������������m��0.1 kg������R��0.5 �������뵼��Ķ�Ħ����������0.4(���Ħ�������ڻ���Ħ����)����Ч����L��0.2 m��Ϊ��ʹ�������ܹ����ڵ������澲ֹ����������ʩ��һ��ֽ���37�������������������ֱ�Ĵų����ʴų�������б���ϻ���б���£��Ÿ�Ӧǿ��B�ķ�Χ�Ƕ��(![]() =0.6,
=0.6,![]() =0.8,gȡ10 m/s2)(������С�������һλ��Ч����)
=0.8,gȡ10 m/s2)(������С�������һλ��Ч����)

���𰸡�2.7T��B��8.9 T
��������
�������֪�����밲�����йص�ƽ�����⣬��ϱպϵ�·ŷķ���ɣ�����ƽ���ϵ����ɵá�
�Ծ�ֹ�Ľ�����Ϊ�о����������������ͼ��ʾ���������Ե���һ����ѹ�����������ֶ����֪�ų�����б���¡�����ƽ����������ͼ����Ħ����Ff�������ϣ���
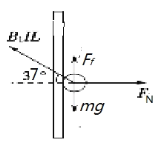
��ƽ�ⷽ�̿ɵ�
B1ILsin 37������B1ILcos 37����mg
��Ħ�����������£���ͼ��
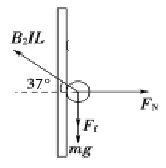
��ƽ�ⷽ�̿ɵ�
B2ILsin 37������B2ILcos 37����mg
�����
I��![]()
�������ݽ��
B1��2.7 T��B2��8.9T��
������Ÿ�Ӧǿ�ȵķ�Χ��2.7T��B��8.9 T��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ