题目内容
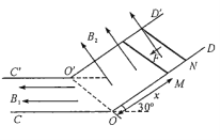
【题目】如图,两根相距![]() 的平行金属导轨OC,
的平行金属导轨OC,![]() ,水平放置于匀强磁场中,磁场方向水平向左,磁感应强度
,水平放置于匀强磁场中,磁场方向水平向左,磁感应强度![]() 。导轨右端O、
。导轨右端O、![]() 连接着与水平面成30的光滑平行导轨OD、
连接着与水平面成30的光滑平行导轨OD、![]() ,OC与OD、
,OC与OD、![]() 与
与![]() 分别位于同一竖直平面内,
分别位于同一竖直平面内,![]() 垂直于OC、
垂直于OC、![]() 倾斜导轨间存在一匀强磁场,磁场方向垂直于导轨向上,磁感应强度
倾斜导轨间存在一匀强磁场,磁场方向垂直于导轨向上,磁感应强度![]() 两根与倾斜导轨垂直的金属杆M、N被固定在导轨上,M、N的质量均为
两根与倾斜导轨垂直的金属杆M、N被固定在导轨上,M、N的质量均为![]() ,电阻均为
,电阻均为![]() ,杆与水平导轨间的动摩擦因数为
,杆与水平导轨间的动摩擦因数为![]() 。现将M杆从距
。现将M杆从距![]() 边界
边界![]() 处静止释放,已知M杆到达
处静止释放,已知M杆到达![]() 边界前已开始做匀速运动。当M杆一到达
边界前已开始做匀速运动。当M杆一到达![]() 边界时,使N杆在一平行导轨向下的外力F作用下,开始做加速度为
边界时,使N杆在一平行导轨向下的外力F作用下,开始做加速度为![]() 的匀加速运动。导轨电阻不计,g取
的匀加速运动。导轨电阻不计,g取![]() 。
。
(1)求M杆下滑过程中,M杆产生的焦耳热Q;
(2)求N杆下滑过程中,外力F与时间t的函数关系;
(3)已知M杆停止时,N杆仍在斜面上,求N杆运动的位移;
(4)已知M杆进入水平轨道直到停止的过程中,外力F对N杆所做的功为15J,求这一过程中系统产生的总热量![]() 。
。
【答案】(1)18.75J;(2)![]() ;(3)3m;(4)24.5J。
;(3)3m;(4)24.5J。
【解析】
(1)M杆匀速运动时受力平衡,由平衡条件可求出M杆匀速运动时的速度,再由能量守恒定律求解M杆产生的焦耳热
(2)N杆下滑时做匀加速运动,根据牛顿第二定律和安培力与速度的关系列式,可求出F与t的关系式。
(3)N杆在斜轨道上滑行的过程中,M杆在水平面上做减速运动。对M杆,根据牛顿第二定律列式可得到加速度与时间的关系,作出M杆的加速度与时间的图象,图象与时间轴所围成的面积表示M杆速度的变化量,根据速度的变化量大小得到M杆停止时所用时间,根据两杆运动的同时性,得到N杆的运动时间,再由位移时间公式求出N杆运动的位移s。
(4)这一过程中系统产生的总热量![]() 等于M杆摩擦产生的热量和N杆产生的焦耳热之和,根据功能关系分别求解得出。
等于M杆摩擦产生的热量和N杆产生的焦耳热之和,根据功能关系分别求解得出。
(1)M杆下滑过程中受到的安培力
![]()
M杆匀速运动时速度最大,此时受力平衡,由平衡条件可得
![]()
代入数据解得
![]()
根据能量守恒有
![]()
代入数据解得
![]()
M杆产生的焦耳热
![]()
(2)N杆下滑时做匀加速运动,t时刻所受的安培力大小
![]()
由牛顿第二定律得:
![]()
联立代入数据解得:
![]()
所以N杆下滑过程中,外力F与时间t的函数关系为![]() 。
。
(3)N杆在斜轨道滑行中,M杆在水平面上做减速运动,根据牛顿第二定律有:
![]()
代入数据解得:
![]() ,
,
即N杆作加速度逐渐增大的减速运动。
作出N杆加速度与时间的图象,如图所示:

可知图中围成的面积是N杆速度的变化量,当N杆停止时,速度的改变量大小为
![]()
设N杆经过时间t恰好停止运动,则有:
![]()
代入数据解得:
t=1s
所以N杆在这一秒内运动的位移为:
![]()
(4)M杆和水平轨道由于摩擦产生的热量即为M杆克服摩擦力所做的功:
![]()
代入数据解得:
![]()
对于N杆,根据动能定理得:
![]()
速度![]() ,代入数据解得
,代入数据解得
![]()
所以两金属棒共同产生的焦耳热
![]()
这一过程中系统产生的总热量
![]()

【题目】在“练习多用电表的使用”实验中:
(1)如图为一正在测量中的多用电表表盘.甲同学利用多用电表的直流 50mA 挡测量电流,则读数为__________mA;
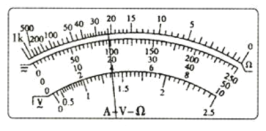
(2)乙同学利用多用电表测量某一只电阻时,他用电阻挡“×100”测量时发现指针偏转角度过小,为了得到比较准确的测量结果,请从下列选项中挑出合理的步骤,操作顺序为__________(填写选项前的字母).
A.将选择开关旋转到电阻挡“×1k”的位置
B.将选择开关旋转到电阻挡“×10 ”的位置
C.将两表笔分别与被测电阻的两根引线相接完成测量
D.将两表笔短接,调节欧姆调零旋钮使指针指向“0 Ω”
(3)丙同学想设计一个实验,测量多用电表“×1Ω” 挡的内部总电阻和内部电源的电动势.指针式多用电表欧姆挡的内部电路是由直流电源、调零电阻和表头相串联而成。给定的器材有:待测多用电表,量程为 100 mA 的电流表,最大电阻为 20 Ω 的滑动变阻器,鳄鱼夹,开关,导线若干. 实验过程如下:
①实验前将多用电表调至“×1 Ω”挡,将红黑表笔短接,调节旋钮,使指针指电阻的零刻度.
②用鳄鱼夹将红、黑表笔固定在图甲的两接线柱上,请用笔画线代替导线将图甲电路连接完整_____.
③调节滑动变阻器,读出多用电表示数 R、毫安表示数 I,求出电流倒数![]() ,记录在下面的表格中,请根据表格数据在图乙的坐标系中描点作图________.
,记录在下面的表格中,请根据表格数据在图乙的坐标系中描点作图________.
R/Ω | 4 | 7 | 10 | 14 | 18 | 20 |
I/10-3A | 8.0 | 67.0 | 60.0 | 52.0 | 45.0 | 43.0 |
| 12.8 | 14.9 | 16.7 | 19.2 | 22.2 | 23.2 |
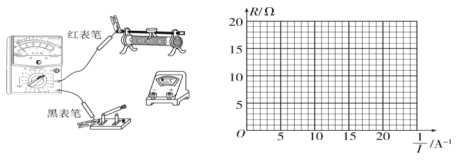
④请通过图线求出多用电表内部电源的电动势为__________V,内部总电阻为__________Ω.(结果保留三位有效数字)
⑤电流表存在一定的内阻,这对实验结果__________(填“有影响”或“无影响”).