Question

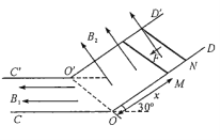
【题目】在交通出行中，人们广泛使用导航软件，一货车正以20 m/s的速度行驶在平直的公路上，司机听到导航右转提示音后2 s开始刹车，刹车后0.5 s内货车的速度随时间变化的规律为v＝20－4t2(m/s)，刹车0.5 s后货车做匀减速直线运动，到达转弯处时恰以5 m/s的速度无侧滑趋势的进入外高内低的弯道。已知弯道宽度为5 m，货车转弯时的轨道半径为50 m，重力加速度g＝10 m/s2，货车可视为质点，θ很小时，tan θ＝sin θ，求：

(1)公路弯道的内外高度差；

(2)根据加速度的定义式推导刹车后0.5 s内货车的加速度与时间的关系式；

(3)司机听到提示音时，货车距弯道的距离(刹车后的0.5 s内可以用初末速度的平均值代替该段时间的平均速度)。

Answer 1

【答案】(1)h＝0.25 m (2) a＝－8t (3)x＝91.75 m

【解析】

(1)货车恰好无侧滑趋势进入弯道

mgtan θ＝m

解得

tan θ＝0.05

由于θ较小，可认为tan θ＝sin θ

h＝dsin θ

解得

h＝0.25 m

(2)货车刹车后0.5 s内，某时刻的速度

v1＝20－4t2

取一小段时间Δt后的速度

v′＝20－4(t＋Δt)2

根据加速度的定义式

a＝

解得

a＝－8 t (m/s2)

(3)货车刹车前运动的位移

x1＝v0t1＝40 m

刹车后0.5 s时的速度

v2＝20－4＝19 m/s

货车刹车后0.5 s内的位移

x2＝t2＝9.75 m

货车刹车0.5 s后的加速度

a＝－8t2＝－4 m/s2

v2－＝2ax3

x3＝42 m

司机听到提示音时，货车距弯道的距离

x＝x1＋x2＋x3＝91.75 m