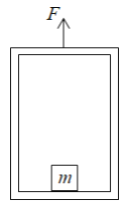
题目内容
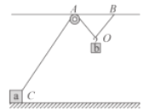
【题目】如图,两弹性轻绳一端系在天花板的O点,另一端分别系着质量均为m的小球a、b,并让两小球都以O'为圆心在同水平面上做匀速圆周运动。已知两弹性绳的弹力都与其伸长量成正比,且原长恰好都等于OO',则( )

A.小球a、b的运动周期相同
B.小球a的向心力大于小球b的向心力
C.小球a、b的线速度大小相同
D.弹性绳1的劲度系数大于弹性绳2的劲度系数
【答案】AD
【解析】
分析小球的受力情况,绳子的弹力和重力的合力提供向心力,列出周期和线速度公式。确定轻绳的弹力和伸长量,根据胡克定律求解劲度系数。
设弹性轻绳与竖直方向的夹角为θ,原长为L,
AC.小球受到绳子的弹力和重力的合力提供向心力,有
![]()
解得运动周期为
![]()
线速度为
![]()
则小球a、b的运行周期相同,线速度大小不等,故A正确,C错误;
B.小球a的绳与竖直方向的夹角小,故小球a的向心力小于小球b的向心力,故B错误。
D.轻绳的弹力
![]()
轻绳的伸长量
![]()
根据胡克定律可知,弹性绳的劲度系数
![]()
小球a的绳与竖直方向的夹角小,弹性绳1的劲度系数大于弹性绳2的劲度系数,故D正确。
故选AD。

练习册系列答案
相关题目