题目内容
11.用图甲所示的电路,测定某蓄电池的电动势和内阻,R为电阻箱,阻值范围0~9999Ω,R0是定值电阻,电压表内阻对电路的影响忽略不计.该同学连接好电路后,闭合开关S,改变电阻箱接入电路的电阻值,读取电压表的示数.根据读取的多组数据,他画出了图乙所示的图象.

(1)电路中定值电阻R0的作用是保护电源,防止短路.
(2)请根据图甲电路图,连接实物图.
(3)在图乙所示图象中,$\frac{1}{U}$=0.10V-1时,外电路的状态最接近断路(选填“正常通路”、“断路”或“短路”)状态.
(4)根据该图象可求得该电池的电动势E=10V,内阻r=5.0Ω.(结果保留两位有效数字)
分析 根据图甲电路图,连接实物图;并根据电路图分析定值电阻的作用.
根据实验的原理得出$\frac{1}{U}$-$\frac{1}{{R}_{0}+R}$关系式,通过图线的斜率和截距求解电源的电动势和内阻.
解答 解:(1)由题意可知,电路中R0的作用是保护电源,防止短路.
(2)根据图甲电路图,连接实物图.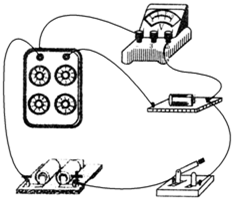
(3)由图可知,当总电阻的倒数为0时,达到0.10V-1;故说明此时外电路电阻无穷大,接近断路;
(4)在闭合电路中,电源电动势:E=U+Ir=U+$\frac{U}{{R}_{0}+R}$r,则$\frac{1}{U}$=$\frac{1}{E}$+$\frac{r}{E}$$\frac{1}{{R}_{0}+R}$,
由图b所示图象可知,截距b=$\frac{1}{E}$=0.1,斜率:k=$\frac{r}{E}$=0.5,
则电源电动势E=$\frac{1}{b}$=10V,电源内阻r=kE=5.0Ω;
故答案为:(1)保护电源,防止短路
(2)如图所示
(3)10;5.0
点评 只用电压表和变阻箱测电动势和内电阻的方法叫“伏欧法”,若用图象解时,基本思路是:用学过的物理定律列出表达式,再结合数学整理表达出有关一次函数式y=kx+b的形式,再求出k和b即可.

练习册系列答案
相关题目
19.物体从静止开始做匀加速直线运动,已知第3s内与第2s内的位移之差是6m,则可知( )
| A. | 物体运动的加速度为3m/s2 | B. | 第2s末的速度为12m/s | ||
| C. | 第1s内的位移为3m | D. | 物体在前4s内的平均速度为15m/s |
6. 如图所示电路中,电源电动势为E、内阻为r,电阻R2为定值电阻,R1为滑动变阻器,A、B为水平放置的电容器的上下两个极板.当滑动变阻器R1处于某位置时,A、B两板间的带电油滴恰好悬浮不动,则下列说法中正确的是( )
如图所示电路中,电源电动势为E、内阻为r,电阻R2为定值电阻,R1为滑动变阻器,A、B为水平放置的电容器的上下两个极板.当滑动变阻器R1处于某位置时,A、B两板间的带电油滴恰好悬浮不动,则下列说法中正确的是( )
 如图所示电路中,电源电动势为E、内阻为r,电阻R2为定值电阻,R1为滑动变阻器,A、B为水平放置的电容器的上下两个极板.当滑动变阻器R1处于某位置时,A、B两板间的带电油滴恰好悬浮不动,则下列说法中正确的是( )
如图所示电路中,电源电动势为E、内阻为r,电阻R2为定值电阻,R1为滑动变阻器,A、B为水平放置的电容器的上下两个极板.当滑动变阻器R1处于某位置时,A、B两板间的带电油滴恰好悬浮不动,则下列说法中正确的是( )| A. | 两极板A、B间正对面积减小其他条件不变时,油滴将向下运动 | |
| B. | 移动R1的滑动触头且其他条件不变时,电压表的读数增大了△U,则电阻R2两端的电压减小了△U | |
| C. | R1滑动触头向左移动且其他条件不变时,带电油滴向上运动 | |
| D. | R1滑动触头向右移动且其他条件不变时,R2上消耗的热功率变小 |
16.关于运动的合成与分解,下列说法正确的是( )
| A. | 合运动的速度等于分运动的速度的矢量和 | |
| B. | 若合运动是曲线运动,则其分运动至少有一个是曲线运动 | |
| C. | 物体的两个分运动若是直线运动,则它的合运动一定是直线运动 | |
| D. | 两个分运动是直线运动,合运动可能是直线运动,也可能是曲线运动 |
3.一个在?=0.1的水平面上向右运动的物体,质量为20kg,运动过程中物体还受到一个水平向左的大小为10N的拉力作用,则它受到的滑动摩擦力为(g取10m/s2)( )
| A. | 10N,水平向右 | B. | 10N,水平向左 | C. | 20N,水平向左 | D. | 20N,水平向右 |
20.由a=$\frac{△v}{△t}$,可知( )
| A. | a与△v成正比 | B. | 物体加速度大小由△v决定 | ||
| C. | 加速度方向与△v方向相同 | D. | $\frac{△v}{△t}$就是加速度 |
1. 如图所示,S1、S2是振动情况完全相同的两个机械波波源,振幅为 A,周期为T,a、b、c三点分别位于S1、S2连线的中垂线上,且ab=bc.某时刻a是两列波的波峰相遇点,c是两列波的波谷相遇点,则( )
如图所示,S1、S2是振动情况完全相同的两个机械波波源,振幅为 A,周期为T,a、b、c三点分别位于S1、S2连线的中垂线上,且ab=bc.某时刻a是两列波的波峰相遇点,c是两列波的波谷相遇点,则( )
 如图所示,S1、S2是振动情况完全相同的两个机械波波源,振幅为 A,周期为T,a、b、c三点分别位于S1、S2连线的中垂线上,且ab=bc.某时刻a是两列波的波峰相遇点,c是两列波的波谷相遇点,则( )
如图所示,S1、S2是振动情况完全相同的两个机械波波源,振幅为 A,周期为T,a、b、c三点分别位于S1、S2连线的中垂线上,且ab=bc.某时刻a是两列波的波峰相遇点,c是两列波的波谷相遇点,则( )| A. | b处质点的振幅为2A | B. | c处质点的位移始终为-2A | ||
| C. | 经过$\frac{T}{4}$,a处质点的位移为0 | D. | 经过$\frac{T}{2}$,a处质点经过的路程为4A |
