Question

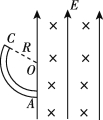
【题目】如图所示，在xOy平面的第二象限有一场强为E的匀强电场，电场的方向平行于y轴向上；在第四象限有一匀强磁场，方向垂直于纸面。平面内其他部分为真空。有一质量为m，电荷量-q的质点由电场左侧平行于x轴以初速度v0射入电场。质点到达x轴上M点时，速度方向与x轴的夹角为θ，M点与原点O的距离为d。接着，质点进入磁场，并从y轴上的N点（图中没有画出）垂直于y轴飞离磁场。不计重力影响。

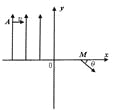
求：（1）A点的横坐标；

（2）匀强磁场的磁感应强度强B的大小和方向；

（3）质点从A到N的时间。

Answer 1

【答案】（1）；（2）；

（3）

【解析】试题分析：质点在第二象限的电场中做类平抛运动，穿过y轴进入第一象限做匀速直线运动交x轴与M点，从M点进入第四象限后做匀速圆周运动，轨迹如图所示，为圆心。

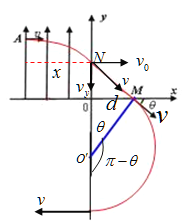
（1）由几何关系可知，质点在电场中做类平抛运动，速度偏角为θ，设质点出电场时的速度为v，竖直方向分速度为vy。

竖直方向分速度：

加速度：

又：

质点在电场中的运动时间：

水平位移：

故A点的横坐标为

（2）质点进入第三象限后，在磁场中做圆周运动，轨迹如图所示，圆心为。

由几何关系可知，轨迹半径

质点做圆周运动的速度：

洛伦兹力提供向心力，根据牛顿第二定律有：

解得磁感应强度：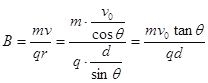

（3）质点在第二象限内做匀速直线运动，运动时间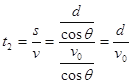

质点在第三象限做圆周运动，由几何关系可知圆心角为

运动时间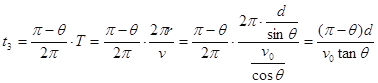

已知质点在第一象限内运动时间

从A到M的总时间为