题目内容
【题目】如图所示,一条长为L的绝缘细线,上端固定,下端系一质量为m的带电小球,将它置于电场强度为E、方向水平向右的匀强电场中,当小球平衡时,悬线与竖直方向的夹角α=45°。
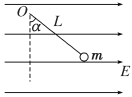
(1)小球带何种电荷?电荷量为多少?
(2)若将小球向左拉至悬线呈水平位置,然后由静止释放小球,则从放手后至最低点的过程中小球做什么运动?经多长时间到达最低点?
【答案】(1)带正电;![]()
(2)放手后小球将做匀加速直线运动;![]()
【解析】
对图示小球进行受力分析,电场力和重力均为恒力,根据平衡可知小球合力,根据牛顿第二定律求得小球的加速度,再根据牛顿运动规律求解即可.
(1)如图所示由题意可知,

小球所受合力为:F合=![]() mg
mg
小球所受电场力与重力大小相等,故有:qE=mg
所以小球所带的电荷量为:q=![]() ,带正电。
,带正电。
(2)将小球向左拉到水平处可知小球所受重力和电场力的合力沿图中虚线方向,而绳在水平方向对球无弹力,故小球将沿虚线方向做匀加速直线运动,

根据牛顿第二定律可知,小球的加速度为:![]()
到达最低点时,小球的位移为![]() L,根据初速度为0的匀加速直线运动规律有:
L,根据初速度为0的匀加速直线运动规律有:![]() L=
L=![]() at2
at2
可得小球运动时间为:![]()

练习册系列答案
相关题目