题目内容
19.有两根阻值分别为R1、R2的电阻丝,分别采用下图所示的四种方法接在同一电源上后,相同时间内产生的热量最大的是( )| A. |  | B. |  | C. |  | D. |  |
分析 因为题中已知电源电压相同,通电时间也相同,所以要比较四个电路产生的热量关系,我们应采用公式$Q=\frac{{U}^{2}}{R}$t去进行分析.由此公式可知,在电压和通电时间都相同时,电流产生的热量与电阻成反比,所以只要分析出四个电路的电阻关系就可以知道它们谁产生的热量最大.
电阻的串联:串联电阻的总电阻比任何一个分电阻的阻值都大;
电阻的并联:并联电阻的总电阻比任何一个分电阻的阻值都小.
解答 解:因为串联后的总电阻比任何一个分电阻的阻值都大,并联后的总电阻比任何一个分电阻的阻值都小,所以在四个电路中,并联电路的总电阻最小.
根据公式$Q=\frac{{U}^{2}}{R}$t可知,当电源电压和通电时间都相同时,电阻小的产生的热量多.因为并联电路的总电阻最小,所以并联电路产生的热量最大.
故选:D.
点评 解答本题需要用公式进行分析,而用哪个公式去分析这值得注意:我们一定要根据题中的条件即等量关系去选择公式,不要一味的只用课本上的公式,有时它的变形式会让我们的分析、解答变得非常简单.本题同时也考查了电阻的串联和并联,是一道比较好的综合题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
9.一物体自t=0时开始做直线运动,其速度图线如图所示.下列选项正确的是( )


| A. | 在0~6s内,物体离出发点最远为30m | |
| B. | 在0~6s内,物体经过的路程为80m | |
| C. | 在0~4s内,物体的平均速率为7.5m/s | |
| D. | 5~6s内,物体所受的合外力做负功 |
10.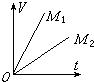 在验证牛顿第二定律的实验中,若保持砂桶和砂子的总质量不变,改变小车内砝码的总质量时,利用纸带上的数据可以算出小车的速度,取其中两次实验的结果作出小车的速度图线,如图所示.前后两次小车与砝码的总质量分别为M1和M2,则M1和M2的关系为( )
在验证牛顿第二定律的实验中,若保持砂桶和砂子的总质量不变,改变小车内砝码的总质量时,利用纸带上的数据可以算出小车的速度,取其中两次实验的结果作出小车的速度图线,如图所示.前后两次小车与砝码的总质量分别为M1和M2,则M1和M2的关系为( )
 在验证牛顿第二定律的实验中,若保持砂桶和砂子的总质量不变,改变小车内砝码的总质量时,利用纸带上的数据可以算出小车的速度,取其中两次实验的结果作出小车的速度图线,如图所示.前后两次小车与砝码的总质量分别为M1和M2,则M1和M2的关系为( )
在验证牛顿第二定律的实验中,若保持砂桶和砂子的总质量不变,改变小车内砝码的总质量时,利用纸带上的数据可以算出小车的速度,取其中两次实验的结果作出小车的速度图线,如图所示.前后两次小车与砝码的总质量分别为M1和M2,则M1和M2的关系为( )| A. | M1>M2 | B. | M1<M2 | C. | M1=M2 | D. | 三者都可能 |
7.在用电压表、电流表测两节干电池串联的电动势和内电阻时,除备有被测电池、开关和足量导线外还有下列仪器可供选择:

A.电流表(0~0.6A)
B.电流表(0~3A)
C.电压表(0~3V)
D.电压表(0~15V)
E.滑动变阻器R1(20Ω,2A)
F.滑动变阻器R2(1 750Ω,3A)
(1)应该选用的仪器是(写出前面的字母)ACE.
(2)在图1方框中画出实验电路原理图.
(3)完成图3实物图连线.
(4)根据表中测量的数据,在如图2所示的坐标轴上画出U-I图象.
(5)从图中可得出电源电动势为2.85 V,内电阻为2.5Ω.

A.电流表(0~0.6A)
B.电流表(0~3A)
C.电压表(0~3V)
D.电压表(0~15V)
E.滑动变阻器R1(20Ω,2A)
F.滑动变阻器R2(1 750Ω,3A)
(1)应该选用的仪器是(写出前面的字母)ACE.
(2)在图1方框中画出实验电路原理图.
(3)完成图3实物图连线.
(4)根据表中测量的数据,在如图2所示的坐标轴上画出U-I图象.
| 实验序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| U/V | 2.70 | 2.50 | 2.30 | 2.00 | 1.80 | 1.62 |
| I/A | 0.08 | 0.16 | 0.25 | 0.36 | 0.45 | 0.50 |
4.关于速度和加速度的关系,以下说法正确的有( )
| A. | 加速度方向为正时,速度一定增大 | |
| B. | 加速度大小不断变小,速度大小可却越来越大 | |
| C. | 加速度方向保持不变,速度方向也保持不变 | |
| D. | 速度变化量越大,加速度越大 |
11.如图所示,一刚性矩形铜制线圈从高处自由下落,进入一水平的匀强磁场区域,然后穿出磁场区域( )

| A. | 若线圈进人磁场过程是匀速运动,则离开磁场过程一定是匀速运动 | |
| B. | 若线圈进入磁场过程是加速运动,则离开磁场过程一定是加速运动 | |
| C. | 若线圈进入磁场过程是减速运动,则离开磁场过程一定是加速运动 | |
| D. | 若线圈进入磁场过程是减速运动,则离开磁场过程一定是减速运动 |
9. Ⅰ在探究“牛顿第二定律”时,某小组设计“双车位移比较法”来探究加速度与力的关系.实验装置如图所示,将轨道分上下双层排列,两小车后的刹车线穿过尾端固定板,由安装在后面的刹车系统同时进行控制(刹车系统未画出).通过改变砝码盘中的砝码来改变拉力大小.通过比较两小车的位移来比较两小车的加速度大小.
Ⅰ在探究“牛顿第二定律”时,某小组设计“双车位移比较法”来探究加速度与力的关系.实验装置如图所示,将轨道分上下双层排列,两小车后的刹车线穿过尾端固定板,由安装在后面的刹车系统同时进行控制(刹车系统未画出).通过改变砝码盘中的砝码来改变拉力大小.通过比较两小车的位移来比较两小车的加速度大小.
已知两车质量均为200g,实验数据如表中所示
试根据该实验的情境,回答下列问题:
(1)两小车的位移S甲、S乙与加速度a甲、a乙的关系满足$\frac{{S}_{甲}}{{S}_{乙}}$=$\frac{{a}_{甲}}{{a}_{乙}}$.
(2)分析表中数据可得到结论:在小车质量相同的情况下,小车的加速度与外力成正比.
(3)该装置中的刹车系统的作用是让两个小车同时运动,同时停车,确保两车的运动时间相等.
 Ⅰ在探究“牛顿第二定律”时,某小组设计“双车位移比较法”来探究加速度与力的关系.实验装置如图所示,将轨道分上下双层排列,两小车后的刹车线穿过尾端固定板,由安装在后面的刹车系统同时进行控制(刹车系统未画出).通过改变砝码盘中的砝码来改变拉力大小.通过比较两小车的位移来比较两小车的加速度大小.
Ⅰ在探究“牛顿第二定律”时,某小组设计“双车位移比较法”来探究加速度与力的关系.实验装置如图所示,将轨道分上下双层排列,两小车后的刹车线穿过尾端固定板,由安装在后面的刹车系统同时进行控制(刹车系统未画出).通过改变砝码盘中的砝码来改变拉力大小.通过比较两小车的位移来比较两小车的加速度大小.已知两车质量均为200g,实验数据如表中所示
| 实验次数 | 小车 | 拉力F/N | 位移s/cm | 拉力比$\frac{F_甲}{F_乙}$ | 位移比$\frac{S_甲}{S_乙}$ |
| 1 | 甲 | 0.1 | 22.3 | 0.50 | 0.51 |
| 乙 | 0.2 | 43.5 | |||
| 2 | 甲 | 0.2 | 29.0 | 0.67 | 0.67 |
| 乙 | 0.3 | 43.0 | |||
| 3 | 甲 | 0.3 | 41.0 | 0.75 | 0.74 |
| 乙 | 0.4 | 55.4 |
(1)两小车的位移S甲、S乙与加速度a甲、a乙的关系满足$\frac{{S}_{甲}}{{S}_{乙}}$=$\frac{{a}_{甲}}{{a}_{乙}}$.
(2)分析表中数据可得到结论:在小车质量相同的情况下,小车的加速度与外力成正比.
(3)该装置中的刹车系统的作用是让两个小车同时运动,同时停车,确保两车的运动时间相等.
