题目内容
12. 如图所示,半径为R的四分之一圆弧支架,支架底ab离地面距离4R,圆弧边缘C处有一个小定滑轮,一轻绳两端分别系着质量为m1m2的物体(可视为质点),挂在定滑轮两边,且m1大于m2,开始时两物体均静止.(不计一切摩擦)求:
如图所示,半径为R的四分之一圆弧支架,支架底ab离地面距离4R,圆弧边缘C处有一个小定滑轮,一轻绳两端分别系着质量为m1m2的物体(可视为质点),挂在定滑轮两边,且m1大于m2,开始时两物体均静止.(不计一切摩擦)求:(1)m1经过最低点a时的速度.
(2)若m1 经过最低点时绳断开,m1 落地点离a的水平距离为多少?
(3)为使 m1 能到达a点m1与m2之间必须满足什么关系?
分析 (1)对两球组成的整体,运用机械能守恒定律列式,并根据经过最低点a时两球沿绳子方向的分速度大小相等,得到它们速度大小的关系,再进行求解;
(2)绳断开后m1做平抛运动,根据平抛运动的规律求m1落地点离a点水平距离S;
(3)当m1经过最低点a时的速度大于等于零时,m1 能到达a点,由上式结果分析.
解答 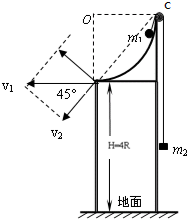 解:(1)如图将m1 的运动分解,则v2=v1sin45°
解:(1)如图将m1 的运动分解,则v2=v1sin45°
m1m2 组成的系统机械能守恒,则得:
m1gR-m2g•$\sqrt{2}$R=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22
解得:v1=2$\sqrt{\frac{({m}_{1}-\sqrt{2}{m}_{2})gR}{2{m}_{1}+{m}_{2}}}$
(2)绳断后m1 做平抛运动,平抛时间为:
t=$\sqrt{\frac{2H}{g}}$=2$\sqrt{\frac{2R}{g}}$
m1 落地点离a的水平距离为:S=v1t=4R$\sqrt{\frac{2({m}_{1}-\sqrt{2}{m}_{2})}{2{m}_{1}+{m}_{2}}}$
(3)为使 m1 能到达a点,必须有:v1≥0
由v1=2$\sqrt{\frac{({m}_{1}-\sqrt{2}{m}_{2})gR}{2{m}_{1}+{m}_{2}}}$≥0
可知当${m}_{1}≥\sqrt{2}{m}_{2}$时m1可到达a点.
答:(1)m1经过最低点a时的速度为2$\sqrt{\frac{({m}_{1}-\sqrt{2}{m}_{2})gR}{2{m}_{1}+{m}_{2}}}$.
(2)若m1 经过最低点时绳断开,m1 落地点离a的水平距离为4R$\sqrt{\frac{2({m}_{1}-\sqrt{2}{m}_{2})}{2{m}_{1}+{m}_{2}}}$.
(3)为使 m1 能到达a点m1与m2之间必须满足的条件是${m}_{1}≥\sqrt{2}{m}_{2}$.
点评 本题根据系统的机械能守恒处理连接体问题,也可以根据动能定理求速度,抓住两球沿绳子方向的分速度相等是解答的关键.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | “嫦娥一号”绕月球表面做圆周运动的周期比绕地球表面做圆周运动的周期大 | |
| B. | “嫦娥一号”绕月球表面做圆周运动的向心加速度比绕地球表面做圆周运动的向心加速度大 | |
| C. | “嫦娥一号”绕月球表面做圆周运动的速度大于 7.9km/s | |
| D. | “嫦娥一号”在月球表面附近所受月球的万有引力小于在地球表面附近所受地球的万有引力 |
 CTMD(中国战区导弹防御体系)是一种战术型导弹防御系统,可以拦截各类型的短程及中程超音导弹.在某次演习中,检测系统测得关闭发动机的导弹在距地面高为H处,其速度为v且恰好水平,反应灵敏的地面拦截系统同时以初速度V竖直向上发射一颗炮弹成功拦截,已知发射时炮弹与导弹的水平距离为s,不计空气阻力,则( )
CTMD(中国战区导弹防御体系)是一种战术型导弹防御系统,可以拦截各类型的短程及中程超音导弹.在某次演习中,检测系统测得关闭发动机的导弹在距地面高为H处,其速度为v且恰好水平,反应灵敏的地面拦截系统同时以初速度V竖直向上发射一颗炮弹成功拦截,已知发射时炮弹与导弹的水平距离为s,不计空气阻力,则( )| A. | V=v | B. | V=$\sqrt{\frac{H}{s}}$v | C. | V=$\frac{s}{H}$v | D. | V=$\frac{H}{s}$v |




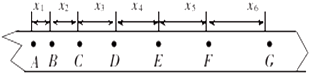 在做“研究匀变速直线运动”的实验时,得到一条纸带如图所示,A、B、C、D、E、F、G为计数点,每两个计数点间还有4个点未画出,xl=1.20cm,x2=1.60cm,x3=1.98cm,x4=2.38cm,x5=2.79cm,x6=3.18cm.
在做“研究匀变速直线运动”的实验时,得到一条纸带如图所示,A、B、C、D、E、F、G为计数点,每两个计数点间还有4个点未画出,xl=1.20cm,x2=1.60cm,x3=1.98cm,x4=2.38cm,x5=2.79cm,x6=3.18cm. 己知电源电动势e=20V,内阻r=5Ω,如图电路接通时标有“3V4.5W”的灯L和内阻R=0.5Ω 的小型直流电动机恰能正常工作,求:
己知电源电动势e=20V,内阻r=5Ω,如图电路接通时标有“3V4.5W”的灯L和内阻R=0.5Ω 的小型直流电动机恰能正常工作,求: 在探究合力的方法时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳.实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.
在探究合力的方法时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳.实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.