题目内容
13. 一列简谐横波沿x轴正方向传播,在x=0与x=2m的两质点振动图线分别如图中实线与虚线所示,由此可得出( )
一列简谐横波沿x轴正方向传播,在x=0与x=2m的两质点振动图线分别如图中实线与虚线所示,由此可得出( )| A. | 该波的波长可能是4m | |
| B. | 该波的周期是5s | |
| C. | 波的传播速度可能是2m/s | |
| D. | 在t=2s时刻,x=2m处的质点正向上运动 |
分析 根据同一时刻两质点的状态,结合波形,确定出两点间距离与波长的关系,求出波长.由图读出周期.由于波的传播方向未知,分两种方向进行分析,求解波速可能的值.
解答 解:A、波沿x轴正方向传播时,在x=0与x=2m的两质点振动图线分别如图中实线与虚线所示,
传播的距离为2m,则传播距离与波长的关系,x=(n+$\frac{1}{4}$)λ,解得:λ=$\frac{2}{n+\frac{1}{4}}$(n=0,1,2,…),
当n=0时,波长λ=8m;当n=1时,波长λ=1.6m.故A错误.
B、该波的周期等于两质点振动的周期为T=4s.故B错误.
C、在x=0与x=2m的两质点振动图线分别如图中实线与虚线所示,则所需要时间为t=n+$\frac{T}{4}$(n=0,1,2,…),那么传播速度v=$\frac{x}{t}$=$\frac{2}{nT+\frac{T}{4}}$=$\frac{2}{4n+1}$m/s,当n=0时,波速v=2m/s;当n=1时,波速v=0.4m/s,故C正确.
D、波沿x轴正方向传播时,当波速为v=1m/s时,即t=2s时刻,则x=2m处的质点才正向上运动.故D错误.
故选:C.
点评 本题要根据两质点的在同一时刻的状态,画出波形,分析距离与波长的关系,再求解波长.要考虑双向性,不能漏解.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
18.在物理学的发展过程中,许多物理学家都做出了重要的贡献,他们也创造出了许多物理学研究方法,下列关于物理学研究方法的叙述中正确的是( )
| A. | 平抛运动、速度、点电荷等都是理想化模型 | |
| B. | 物理学中所有物理量都是采用比值法定义的 | |
| C. | 法拉第最先提出电荷周围存在电场的观点 | |
| D. | 电荷的周围既有电场也有磁场,反映了电和磁是密不可分的 |
5.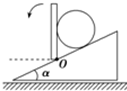 如图所示,一小球在斜面上处于静止状态,不考虑一切摩擦,如果把竖直挡板由竖直位置缓慢绕O点转至水平位置,则此过程中球对斜面的压力F1和球对挡板的压力F2的变化情况是( )
如图所示,一小球在斜面上处于静止状态,不考虑一切摩擦,如果把竖直挡板由竖直位置缓慢绕O点转至水平位置,则此过程中球对斜面的压力F1和球对挡板的压力F2的变化情况是( )
 如图所示,一小球在斜面上处于静止状态,不考虑一切摩擦,如果把竖直挡板由竖直位置缓慢绕O点转至水平位置,则此过程中球对斜面的压力F1和球对挡板的压力F2的变化情况是( )
如图所示,一小球在斜面上处于静止状态,不考虑一切摩擦,如果把竖直挡板由竖直位置缓慢绕O点转至水平位置,则此过程中球对斜面的压力F1和球对挡板的压力F2的变化情况是( )| A. | F1一直减小,F2先减小后增大 | B. | F1先减小后增大,F2先增大后减小 | ||
| C. | F1和F2都一直减小 | D. | F1和F2都一直增大 |
2.电梯正以2m/s的速度匀速上升,从电梯内2m高的天花板上脱落一枚螺钉,掉在电梯地板上,其所用时间为(取g=10m/s2)( )
| A. | $\sqrt{\frac{2}{5}}$s | B. | 大于$\sqrt{\frac{2}{5}}$s | C. | 小于$\sqrt{\frac{2}{5}}$s | D. | $\frac{\sqrt{2}}{5}$s |